社会统计学中通过消减误差比例来计算λ系数的方法及应用

λ 系数就是基于消减误差比例的思想构建的列联相关系数。 利用消减误差比例的思想构建列联相关系数的关键是确定E1 和E2，现举一例予以说明。

假设在某学校随机抽取了200 名学生，男女各100 名，对他们是否愿意参加课外辅导的调查结果如表4.10 所示。 从表4.10 可以看出，学生们是否愿意参加课外辅导与性别是相关的。 要计算这两个变量的相关系数，应先定义E1 和E2。

表4.10　学生是否愿意参加课外辅导的统计结果

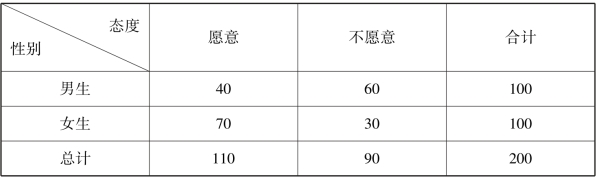
假设只知道调查样本中有110 个学生愿意参加课外辅导，90 人不愿意参加。 在这种情况下要猜测每一个学生的态度，可以猜测为所有的学生都愿意参加课外辅导。 因为这样能猜对110 人，猜错90 人。 此时形成的误差E1 为：

E1 ＝200 － 110 ＝90（人）

如果在知道了不同性别的学生对参加课外辅导的态度分布的情况下再对每个学生的态度进行猜测，猜测的方法是：所有的男生均猜测为不愿意，所有的女生均猜测为愿意。 这样能猜对130 人，猜错70 人。 此时形成的误差E2 为：

E2 ＝（100 － 60） ＋（100 － 70）＝70（人）

则消减误差比例为：

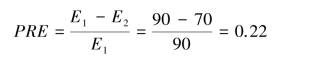
即利用性别来猜测学生对参加课外辅导的态度可以消减22%的误差。 根据上述定义E1 和E2 的方法可以推导出计算列联表中两个变量之间λ 系数的公式。 下面讨论λ系数中E1 和E2 的定义方法。

（1）E1 的定义

以列联表4.2 为例，在未知y 与x 相关之前，如果要去预测y 值，唯一可以参考的则是y 本身的分布，即关于y 的边缘分布。 当预测每一个y 值时，用边缘分布中的众数来猜测所有个体要比用其他取值来猜测产生的误差小。 设变量y 众数的频次为max（n∗j），则猜测误差E1 为：

（2）E2 的定义

当知道y 与x 相关之后，如果再去预测每一个y 值，显然要先看它属于x 的哪一类，然后根据这一类中y 的众数去猜测它，即用条件分布中的众数去预测y，这样猜中的频次最多，误差最小。

设x ＝x1 时，条件分布中众数的频次为max（n1j）；

x ＝x2 时，条件分布中众数的频次为max（n2j）；

︙

x ＝xi 时，条件分布中众数的频次为max（nij）；

︙

x ＝xr 时，条件分布中众数的频次为max（nrj）。

则猜测误差E2 为：

（3）λ 系数的计算

综上，用变量x 来猜测y 的消减误差比例λy 系数的计算公式为：(www.xing528.com)

当变量x 和y 不相关时，边缘频率分布等于条件频率分布，所有的众数均在同一列，因此有：

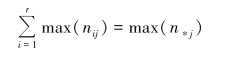
代入式（4.8）得：

λy ＝0

当变量x 和y 完全相关时，表4.2 中的每一行都只有一个不为0 的频次，因此有：

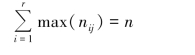
代入式（4.8）得：

λy ＝1

即当变量x 和y 不相关时，λy ＝0；当变量x 和y 完全相关时，λy ＝1。

从上述λy 系数的计算中可以看出，消减误差比例是基于借助x 猜测y 来定义的。 如果借助y 来猜测x，定义的E1 和E2 是不同的，计算出的λ 系数也是不同的，即λ 系数具有不对称性。

参照式（4.8），借助y 来猜测x 的λx 系数的计算公式为：

如果两个变量之间具有明确意义上的因果关系，习惯上将x 设为自变量，将y 设为因变量。 如果两个变量之间的因果关系不太明确，可以计算λy 和λx 的加权平均数作为两个变量的列联相关系数，计算公式如下：

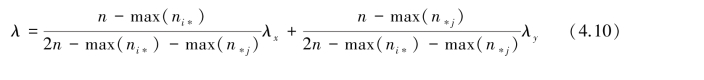
【例4.2】　请计算表4.1 中年龄段与电视节目类型间的λ 系数。

解　由交叉列表可以看出，年龄段与电视节目类型是相关的。

设节目类型为x，年龄段为y，则：

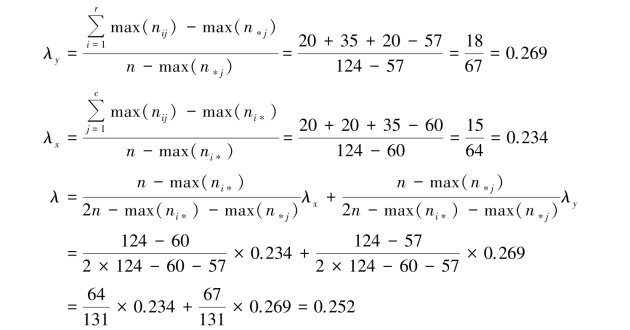
即年龄段和电视节目类型的λ 系数为0.252。

【例4.3】　为了研究饮食习惯与地区之间的关系，作了共100 人的抽样调查（见表4.11），请计算地区和饮食习惯间的λ 系数。

表4.11　饮食习惯与地区的抽样调查结果

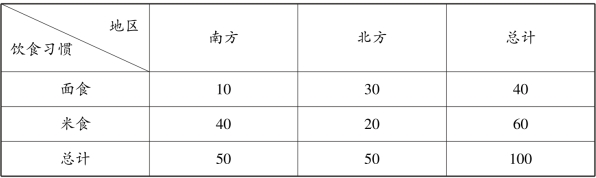
解　为了检验饮食习惯是否与地区相关，设变量地区为x，饮食习惯为y，则：

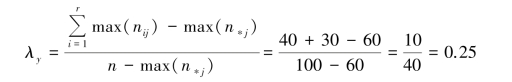
结果表明，饮食习惯与地区间是相关的，如果用地区去解释饮食习惯的差异，可以减少预测误差的25%。