消减误差比例的统计思想在社会统计学中的应用

消减误差比例的基本思想是：在没有任何可参考信息的情况下猜测一个事物时会有很大的盲目性，而借助一个与被猜测的事物有关的事物来进行猜测，就会减少盲目性，提高猜测的准确性。 如果两个变量相关，则借助一个变量去猜测另一个变量时会消减猜测误差。消减的误差大，说明两个变量之间的密切程度高；消减的误差小，说明两个变量之间的密切程度低。 这样，消减误差的大小便可以作为测量两个变量之间关系密切程度的指标。

设两个变量x 和y，观察的个体总数为n。 现直接猜测每个个体在变量y 上的取值，这是一种盲目猜测，必然产生误差，设猜测n 个个体所产生的总误差为E1。 如果每个个体在变量x 上的取值是已知的，则可以借助个体在变量x 上的取值来猜测其在变量y 上的取值，设此时产生的总误差为E2。 则消减误差比例的计算公式为：

当变量x 与y 不相关时，由于知道x 与否无助于y 的预测，则借助x 来猜测y 所产生的误差与直接猜测y 产生的误差相同，即E1 ＝E2，因此：

同理，当变量x 与y 完全相关时，借助x 能够准确地计算y，不产生任何误差，即E2 ＝0，因此：

可见，PRE 是一个取值在0 和1 之间的相对数。 其值越接近1，说明两个变量的相关性越强；其值越接近0，说明两个变量的相关性越弱。

例如，假设有4 名学生的平均身高是170 厘米。 若要猜测每名学生的身高，唯一可以参考的信息就是平均身高，此时只能猜测每名学生的身高均为170 厘米。 实际上，这4 名学生的身高分别为181 厘米、176 厘米、162 厘米、161 厘米。 则猜测所产生的总误差为：

E1 ＝（181 － 170） ＋（176 － 170） ＋（170 － 162） ＋（170 － 161）＝34（厘米）

若此时再假设前两名学生为男生，平均身高是178.5 厘米；后两名学生为女生，平均身高是161.5 厘米。 现在再来猜测这4 名学生的身高时就可以以性别作为参考。 此时，男生的身高均猜测为178.5 厘米，女生的身高均猜测为161.5 厘米，则猜测所产生的总误差为：

E2 ＝（181 － 178.5） ＋（178.5 － 176） ＋（162 － 161.5） ＋（161.5 － 161）＝6（厘米）

消减误差比例为：

可见，借助性别来猜测学生的身高可以消减82%的误差，这说明性别与身高有较强的相关关系。(www.xing528.com)

若假设4 名学生的身高是两名男生均为175 厘米，两名女生均为165 厘米，平均身高仍为170 厘米，计算此时的E1，E2 和消减误差比例分别为：

E1 ＝2 × （175 － 170） ＋2 × （170 － 165）＝20（厘米）

E2 ＝2 × （175 － 175） ＋2 × （165 － 165）＝0（厘米）

此时，性别与身高是完全相关的，借助性别可以准确地猜测学生的身高。

消减误差比例公式中E1，E2 的具体定义，不仅在不同层次的变量有所不同，而且对于同一层次的变量，也可以有所不同。 下面介绍列联表中根据两种E1 和E2 的定义方法所形成的两种系数：λ 系数和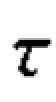系数。

【案例】

相关系数的应用

在某城市社区随机抽取了200 名60 岁以上的老年人，男女各100 名，他们对去老年公寓养老的态度分布如下表所示。

从表中可以看出，老年人是否愿意去老年公寓养老与性别是相关的。 那么，这两个变量之间的相关程度怎么样呢？ 这就需要计算二者的相关系数。 下面将介绍两种相关系数：λ 系数和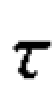系数。