【摘要】：在列联表中，可以通过比较条件分布来研究类别变量之间的关系。从频率分布来看，两个变量相互独立的表现是条件分布等于边缘分布。因此，列联表中两个变量相互独立可以表达为：将式（4.2）等号左侧的分子、分母同乘以n 得：上式可以变换为：即式（4.4）说明，若两个变量相互独立，则在频率分布的列联表中，联合分布等于边缘分布的乘积，其一般形式如表4.9 所示。表4.9两个变量相互独立的列联表
在列联表中，可以通过比较条件分布来研究类别变量之间的关系。 当一个变量取不同类别时，另一个变量的分布有差异，即说明这两个变量是相关的。 当一个变量取不同值时，另一个变量的条件分布只有微小差异或者根本无差异，则认为这两个变量不相关，即两个变量相互独立。 例如，根据表4.7 中的每一行，可以比较出三代人的喜爱是否有所不同，三代人的百分比依次为：
戏曲：0.741→0.250→0.035
歌舞：0.185→0.500→0.614
球赛：0.074→0.250→0.351
可见，随着代际的年轻化，戏曲喜爱的比例逐渐下降，而歌舞和球赛却越来越受到欢迎，从而得出节目类型的喜爱程度与代际有关的结论，即节目类型与年龄段这两个变量是相关的。
现在设想，如果统计的结果是三代人的百分比保持不变，即：
戏曲：0.741→0.741→0.741
歌舞：0.185→0.185→0.185
球赛：0.074→0.074→0.074
显然，如果各节目类型三代人的喜爱比例是一样的话，那就表示节目类型与年龄段这两个变量之间是不相关的，即两个变量相互独立。
从频率分布来看，两个变量相互独立的表现是条件分布等于边缘分布。
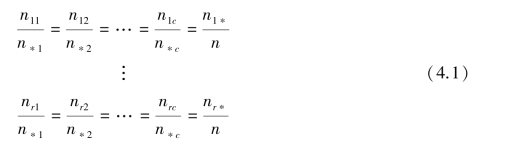(www.xing528.com)
因此，列联表中两个变量相互独立可以表达为：
将式（4.2）等号左侧的分子、分母同乘以n 得：
上式可以变换为：
即
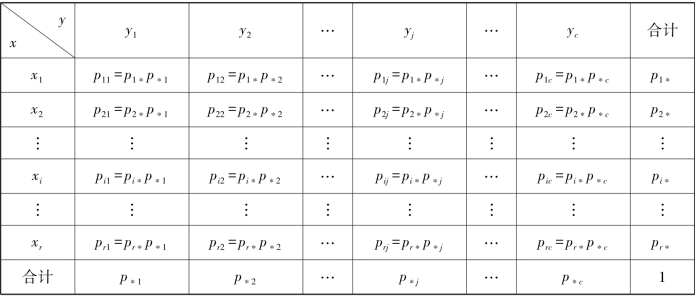
式（4.4）说明，若两个变量相互独立，则在频率分布的列联表中，联合分布等于边缘分布的乘积，其一般形式如表4.9 所示。
表4.9 两个变量相互独立的列联表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
