社会统计学：列联表分布

（1）联合分布

第3 章第3.1 节介绍了单变量的分布，对于两个变量而言，为了知道分布，集合中的变量值必须同时具有x 和y 两个变量的取值：

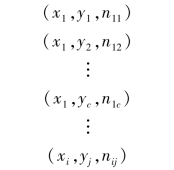
当集合中最后一项nij表示的是频次时，列联表就是联合频次分布表；当集合中最后一项表示的是频率pij时，则列联表就是联合频率分布表。 可见，列联表中间部分的数据nij或pij都是由两个变量共同决定的，所以称为联合分布。

（2）边缘分布

如果对联合分布进行简化研究，只研究其中某一变量的分布，而不管另一变量的取值，这样就得到边缘分布。

关于y 的边缘分布：把联合分布中的频次或频率按列加总起来，就得到关于y 的边缘分布，即列联表4.2 和表4.3 中最下面一行n∗j或p∗j就是变量y 的边缘分布。

同理，关于x 的边缘分布：把联合分布中的频次或频率按行加总起来，就得到关于x的边缘分布，即列联表4.2 和表4.3 中最右面一列ni∗或pi∗就是变量x 的边缘分布。

（3）条件分布

如果将一个变量取固定值，则另一个变量的分布就是条件分布。 在表4.2 中，每一行的数据是在变量x 取固定值时变量y 的频次的条件分布，每一列的数据是在变量y 取固定值时变量x 的频次的条件分布。 如果变量x 共有r 个取值，变量y 共有c 个取值，那么从理论上来说，就可以有r＋c 个条件分布。 使用条件分布的目的是看当一个变量取不同类别时另一个变量的分布是否有差异。 这种差异通过频次分布难以展现，所以条件分布大多采用频率分布。

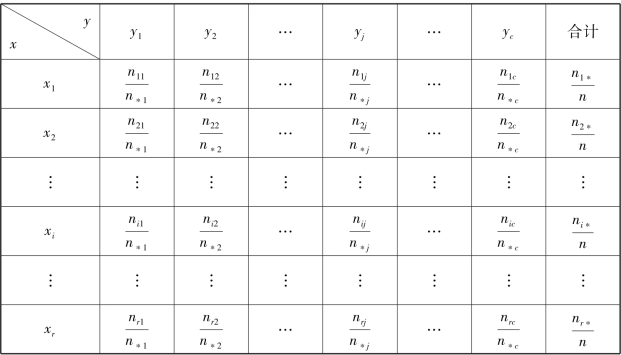
在列联表4.2 中，用单元格的频次除以对应列的总频次，即nij／n∗j构成的分布称为关于变量x 的条件分布，也就是变量y 取固定值时x 的分布，如表4.5 所示。

表4.5　关于x 的条件分布

(www.xing528.com)

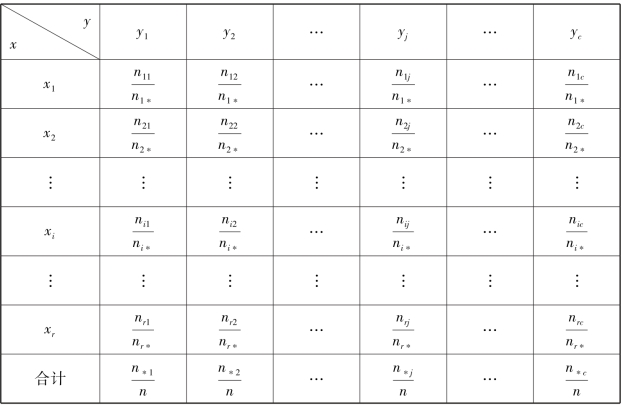
同理，在列联表4.2 中，用单元格的频次除以对应行的总频次，即nij／ni∗构成的分布称为关于变量y 的条件分布，也就是变量x 取固定值时y 的分布，如表4.6 所示。

表4.6　关于y 的条件分布

【例4.1】　根据表4.1 的数据分别求关于年龄段和节目类型的条件分布。

解　用表4.1 单元格中的频次除以年龄段的边缘分布，即得到关于节目类型的条件分布，如表4.7 所示。

表4.7　关于节目类型的条件分布表

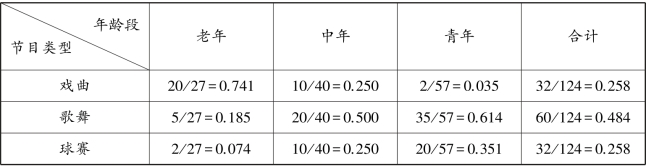
可见，在不同年龄段中，各电视节目类型所占比例有很大差异。

用表4.1 单元格中的频次除以节目类型的边缘分布，即得到关于年龄段的条件分布，如表4.8 所示。

表4.8　关于年龄段的条件分布表

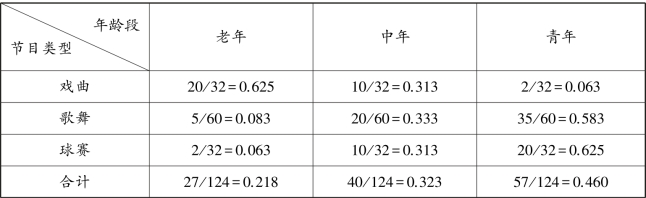
可见，在不同电视节目类型中，各年龄段所占比例有很大差异。