住房面积分布的四分位差计算结果

对于测量层次在定序以上的变量，可以用四分位差来描述变量分布的离散程度。 将数据按大小顺序排成数列以后，从下向上数处于25%位置上的值称为下四分位数，用Q25表示；从下向上数处于75%位置上的值称为上四分位数，用Q75表示。 上下四分位数之差即为四分位差，一般用Q 表示。

四分位差反映了中间50%数据的分散程度，数值越小，说明中间的数据越集中；数值越大，说明中间的数据越分散。 它的优点是既比较好地说明了数据的离散状况，又减少了极值对数据总体造成的影响。 由于中位数处于中间位置，因此四分位差在一定程度上说明了中位数的代表性。

（1）未分组数据四分位差的计算

计算四分位差要先计算上下四分位数，根据四分位数的定义可得：

如果四分位数所在位置是整数，则四分位数就是该位置上的值。 如果是小数，且小数位为0.5，则四分位数取该位置两侧值的平均数。 如果是在0.25 或0.75 的位置上，则四分位数等于该位置下侧值加上按比例分摊位置两侧数值的差值。 具体计算方法见例3.7。

【例3.7】　下面的一组数据是某单位49 名职工的住房面积（单位：平方米），请计算住房面积分布的四分位差。

33　42　42　48　48　52　55　58　62　65　65　65　66　66　66　66　68　68 68　68　68　70　70　70　72　72　72　72　75　75　75　76　76　78　85　87　90 92　95　98　103　109　110　112　118　125　130　178　179

解　n ＝49

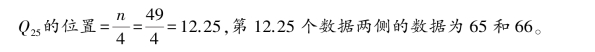
则下四分位数为：

则上分位数为：

Q75 ＝87 ＋0.75 × （90 － 87）＝89.25

由此，四分位差为：

Q ＝Q75 － Q25 ＝89.25 － 65.25 ＝24

即这个单位职工住房面积中间50%数据的离散范围是24 平方米。

（2）分组数据四分位差的计算(www.xing528.com)

对于分组数据，上下四分位数的计算与中位数的计算方法基本相同。 计算公式为：

下四分位数

其中，L 是处于25%位置上的值所在组的下限，n 是处于25%位置上的值所在组的频次，Cf↑是L 以下的累计频次，h 为组距，N 为数据总个数。

上四分位数

其中，L 是处于75%位置上的值所在组的下限，n 是处于75%位置上的值所在组的频次，Cf↑是L 以下的累计频次，h 为组距，N 为数据总个数。

根据式（3.11）和式（3.12）计算出上下四分位数后，再利用式（3.8）计算四分位差。

【例3.8】　请利用表3.9 的数据计算居民家庭住房面积分布的四分位差。

解　①求下四分位数。

从下向上数25%的位置为：883×25%＝221，第221 个数据在40 ～60 平方米的组。 因此，L ＝40，n ＝430，Cf↑＝134，h ＝20，N＝883。

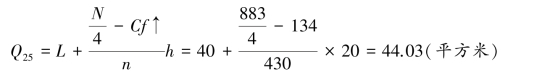
②求上四分位数。

从下向上数75%的位置为：883×75%＝662，第662 个数据在60 ～80 平方米的组。 因此，L ＝60，n ＝198，Cf↑＝564，h ＝20，N＝883。

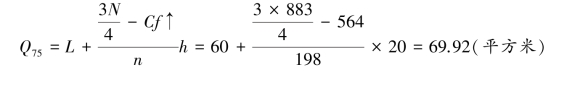
③求四分位差。

Q ＝Q75 － Q25 ＝69.92 － 44.03 ＝25.89（平方米）

即调查样本中有50%的人住房面积分布在44.03 和69.92 平方米之间，他们家庭住房面积分布的四分位差为25.89 平方米。