计算算术平均值 - 社会统计学

算术平均值也称平均值或均值，是全部数据的平均水平。 算术平均数主要适用于尺度变量。 用算术平均数作为变量的集中值，不仅考虑到变量值的频次、次序，而且还考虑到它的大小。 数据资料中任何频次、次序和数值大小的变化，都会引起算术平均数的改变，因此它是灵敏的，也是对资料所提供信息运用得最充分的。

（1）未分组数据算术平均值的计算

1）根据原始数据计算算术平均值

当原始数据比较少时，可直接累加观察值，除以观察值总数，以求得均值，计算公式为：

其中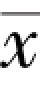， 为平均值，为所有观察值的总和，n 为观察值的个数。

【例3.3】　已知5 名男性的年龄分别为：35，41，55，48，29（单位：岁）；5 名女性的年龄分别为：23，38，18，40，51（单位：岁）。 分别计算他们的平均年龄。

解

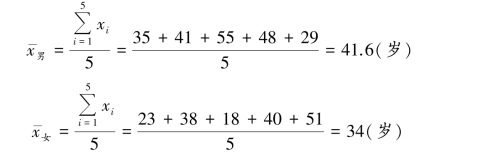
即这5 名男性的平均年龄为41.6 岁，5 名女性的平均年龄为34 岁。

2）根据频次分布计算算术平均值

如果数据已经存在于频次分布表中，则可根据频次分布表中的数据计算算术平均值。 设变量有k 个取值xi（i＝1，2，…，k），每个取值出现的频次为ni（i＝1，2，…，k）。 利用频次分布数据计算平均值的公式为：

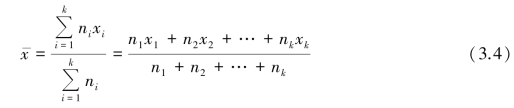(www.xing528.com)

【例3.4】　表3.11 是某年级的成绩分布情况，请计算他们的平均成绩。

表3.11　某年级的成绩分布情况

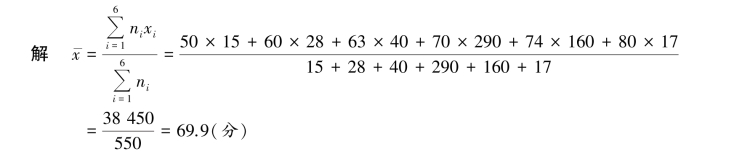
即该年级的平均成绩为69.9 分。

（2）分组数据算术平均值的计算

【例3.5】　根据表3.9 的数据计算被调查者住房面积的平均值。

解　根据各组的上下限计算各组的组中值为：

b1 ＝10，b2 ＝30，b3 ＝50，b4 ＝70，b5 ＝90，b6 ＝110，b7 ＝130，b8 ＝150，b9 ＝170。

即被调查者的平均住房面积为58.47 平方米。