社会统计学：中位数的计算方法与示例

中位数（Me）是位于数列中点的数值，它恰好把全部数据分为两半，比它大的数据与比它小的数据个数正好相等。 因为确定中位数需要比较数据的大小，所以只有测量层次在定序以上的变量才可以使用。 但如果一个序列变量的取值很少，也不适合用中位数作为集中趋势来概括全部数据。 实际上，中位数适用于取值很多的序列变量和尺度变量。

（1）未分组数据中位数的计算

1）根据原始数据计算中位数

对于原始数据，只要将数据按大小顺序排成数列便可以找到中位数。

2）根据频次分布计算中位数

当原始数据很多时，这时可根据分布来计算中位数。

表3.10　××年级学生的成绩分布

(www.xing528.com)

根据表3.10，中位数的位置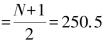，则中位数Me ＝中。

（2）分组数据中位数的计算

在分组数据中，因为没有了数据的原始值，所以无法直接寻找中位数，需要先找到中位数组，第个数据所在的组为中位数组。 确定中位数组以后，利用式（3.2）计算中位数：

其中，L 是中位数组的下限，h 是组距，n 是中位数组的频次，N 为数据总个数，Cf↑是L 以下的累计频次。

【例3.2】　根据表3.9 的数据计算中位数。

解　由表3.9 可知：N＝883，则＝441.5，因此第442 个数据所在的40 ～60 的组是中位数所在的组。

即表3.9 中住房面积的中位数为54.3 平方米。