社会统计学：变量和分布解析

【案例】

人口老龄化

据国家统计局发布的数据显示，截至2018 年末，我国最新的老年人口数据为：60 岁及以上人口24 949 万人，占总人口的17.9%；65 岁及以上人口16 658 万人，占总人口的11.9%。 对比2017 年末，我国60 岁及以上人口在2018 年增长了859 万。

2.49 亿老年人口是个什么概念？ 按照《2018 年中国统计年鉴》的数据，2.49 亿老年人口比巴西的人口总数还高4 000 万，约等于俄罗斯和菲律宾人口的总和，是英国总人口的3.77 倍，是10 个澳大利亚人口总和。

山东省成为全国老龄人口数量最多的省份。 2017 年，山东省60 岁及以上老年人口2 137.3万人，占山东省总人口的21.4%，高出全国平均水平4.0 个百分点；65 岁及以上老年人口达1 399.8 万人，占山东省总人口的14.0%，高出全国平均水平2.6 个百分点。

上海是中国老龄化率最高的地区。 2017 年底上海户籍常住人口中65 岁及以上老年人口达到315.06 万人，户籍人口老龄化率为21.8%，即平均不到5 个户籍人口中就有1个65 岁及以上的老人。 而60 岁及以上老年人口有483.60 万人，占比更高达33.2%，即每不到3 个户籍人口中就有1 位60 岁及以上的老人。

（1）变量的特征

研究对象的每个个体都具有很多属性和特征。 例如，每个人都有身高、体重、年龄、学历等特征。 这些在不同个体上具有不同表现的特征就称为变量。 统计学中变量的定义与物理学中变量的定义不尽相同。 物理学中的变量是指某个个体特征随时间发生变化，这个特征叫作变量。 如一颗射出的子弹飞行距离随时间发生变化，飞行速度随时间发生变化，子弹的飞行距离和飞行速度都可以视为变量。 统计学中的变量在同一个体上是相对稳定的，在不同个体上表现出变化。 如人的文化程度就某个人而言在调查时是确定的，但在不同人的身上有不同的表现。 这类变量也称随机变量。 例如，家庭类型可以分为：

①核心家庭：由一对夫妻或加上其他未婚成员构成的家庭。

②直系家庭：由一对夫妻和他们的父母及子女组成的家庭，家庭中应包括三代人，或者两对不同辈分的夫妻。

③大家庭：含有三对及以上夫妻的家庭。

④断代家庭：由祖辈与未婚孙辈两代人构成的家庭。

⑤单亲家庭：由父母一方与未婚子女构成的家庭。

⑥单身家庭：由一个成年人构成的家庭。

⑦其他家庭。

如果把家庭类型视为一个变量，上述7 个分类就是这个变量的取值。 变量的取值具有两个特征：

一是完备性。 完备性是指变量的取值必须涵盖全部的个体，也就是每个个体的特征都应成为变量的取值。 只有这样，才能使全部个体都进行归类。 上述对家庭类型划分的前6 项包含了绝大部分的家庭类型，但有些特殊的类型没有被包含进去，如只有未婚的兄弟姐妹在一起生活的家庭。 为使家庭类型这一变量具有完备性，应在变量取值中增加“其他家庭”一项。 我们比较以下两个变量的取值表（表3.1 和表3.2）。

表3.1

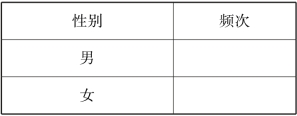
表3.2

显然，表3.1 对于变量“性别”所列举的可能值是完备的，而表3.2 对于变量“收入”所列举的可能值则是不完备的，因为收入在1 001～1 999 元的观察值无处归类。

二是互斥性。 互斥性是指变量的取值之间不能有交集。 若在家庭类型中增加一项“空巢家庭”，将由一对老夫妻构成的家庭区分出来，似乎也合理。 但在上述核心家庭的定义中就包含了空巢家庭，当然也包含了婚后无子女的丁克家庭，此时增加“空巢家庭”就会造成变量取值的不互斥。 我们比较表3.3 和表3.4 两个变量的取值表，显见表3.3 中人数是互斥的，因为人数是离散型定距变量。 组界上的从5 人增至6 人和从10 人增至11 人，中间的小数都不会存在观察对象。 而表3.4 组界上的1 000 元、2 000 元都同时属于两类，所以分类是不互斥的。 但在实际工作中，有时也采用表3.4 的形式。 这时为了满足互斥性，一般增加“上组界不包括在内”的约定。 也就是说，凡收入为1 000 元者，归入1 000～2 000 元档，凡收入为2 000 元者，归入2 000 元以上档。

表3.3

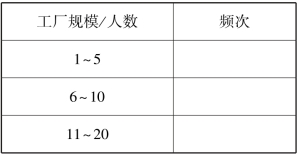
表3.4

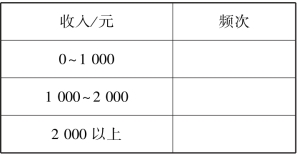
变量的上述两个特征保证了任何一个个体只能具有变量的一个取值。 如果是无序变量，每个个体都会被归入一定的类别中。 如果是有序类别变量，每个个体只能具有一个等级。 当然，每个类别或等级中可能包含很多个体。 如果是尺度变量，每个个体的值都要包含在变量的取值范围之内。

（2）变量的分布

变量的分布是指个体在变量取值上的分布。 对于一组观察值，一般用频次分布、频率分布和累计频率分布3 种方法描述变量的分布。

1）频次分布

变量取值与取值上拥有的个体数的集合称为频次分布。 如果变量x 有m 个取值，分别为x1，x2，…，xm，每个取值上拥有的个体数分别为n1，n2，…，nm，则这个变量的频次分布可以表示为：

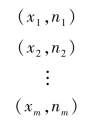
也可以表示为：

例如，在某城市调查了1 000 户家庭，7 种家庭类型户数的频次分布为：

（核心家庭，707 户）

（直系家庭，182 户）

（大家庭，7 户）

（断代家庭，9 户）

（单亲家庭，37 户）(www.xing528.com)

（单身家庭，15 户）

（其他家庭，43 户）

2）频率分布

变量取值与取值上拥有的个体数的频率的集合称为频率分布。 设n ＝n1＋n2＋…＋nm，则频率分布可以表示为：

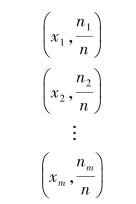
也可以表示为：

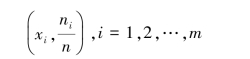
将频率分布的频率乘以100%，就是百分比。

例如，上述1 000 户家庭，7 种家庭类型户数的频率分布为：

（核心家庭，0.707）

（直系家庭，0.182）

（大家庭，0.007）

（断代家庭，0.009）

（单亲家庭，0.037）

（单身家庭，0.015）

（其他家庭，0.043）

3）累计频率分布

将上述频率分布中的频率按照变量取值的排列顺序逐项累加就形成了累计频率分布。 累计频率分布可以表示为：

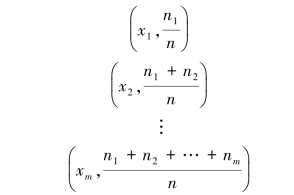
也可以表示为：

例如，上述1 000 户家庭，7 种家庭类型户数的累计频率分布为：

（核心家庭，0.707）

（直系家庭，0.889）

（大家庭，0.896）

（断代家庭，0.905）

（单亲家庭，0.942）

（单身家庭，0.957）

（其他家庭，1）

【案例】

在一项有关城市住房问题的研究中，研究人员在甲、乙两个城市各抽样调查300 户，其中的一个问题是：“您对您家庭目前的住房状况是否满意？”要求回答的类别依次如下：

1.非常不满意；

2.不满意；

3.一般；

4.满意；

5.非常满意。

调查结果的频次和频率分布如表3.5 所示。

表3.5　甲、乙城市家庭对住房状况评价的频次频率分布表

通过上述3 种分布可以清楚地展现数据的分布特征和统计规律。

上述变量分布的表示方法只适用于类别变量。 例如，文化程度、职业、职称等。 这样的变量只有少数几个取值，因此描述变量的分布比较容易。 对取值很多的尺度变量，上述描述分布的方法就不再适用了，如以元为单位来描述人们的月收入。 目前，个人月收入的分布范围可能是从零元到几十万元。 这个变量有几十万个取值，如果调查人数为数千人，则每个取值上平均不到一个人，若按照上述方法列出每个取值以及该取值所对应的人数，不仅工作量很大，而且显示不出统计规律，可以说毫无意义。 通常将变量的取值划分成段，如年龄段、收入段，再累计该段中的人数来表示变量的分布。