违约率和评级：结构金融学的违约风险评估

关于违约风险的评估，主要分为违约率和回收率两大部分。违约率与评级密不可分，较高的评级往往有着较低的违约率。

（一）评级

1.信用评级及符号含义

违约风险是指交易对手或债务当事人未能履行合约所规定的义务或债务人的信用评级发生变化而给债券人或金融产品的持有人带来的风险。具体来说，违约风险的度量包括两个因素：一是违约概率和信用状况发生变化的概率，二是违约损失率的估计。

信用评级是对主体违约风险的评估。信用评级种类繁多，不同种类信用评级的侧重点不同。总的来说，主要包括主体信用评级和债券信用评级两大类。主体信用评级是指评级机构对发行人整体信用水平的评定，以企业为主要评价对象，关注企业的财务风险和经营风险；债券信用评级表达了评级机构对一个债务人关于特定债务证券或其他金融凭证的信誉的评定，以企业发行的有价债券为评价对象，关注特定债券的违约风险和违约损失风险。

来自不同机构的评级传达了不同的信息。目前，标准普尔公司、穆迪投资者服务公司和惠誉国际信用评级公司并称为世界三大评级机构。标准普尔评级（从AAA到C）主要是对发行人违约可能性的意见，穆迪评级（从Aaa到C）倾向于反映该机构对预期损失（违约率乘以损失严重性）的意见。而惠誉评级（从AAA到C）侧重于金融机构的评级，反映对发行人偿债能力的评估意见。

我们采用中国人民银行下发的《信贷市场和银行间债券市场信用评级规范》中规定的符号及对应含义，来表明发债主体及特定债券的违约风险情况。

中长期债券信用评级等级划分为三等九级，符号表示为AAA、AA、A、BBB、BB、B、CCC、CC、C，如表5-1所示。

表5-1　中长期债券信用评级等级划分表

注：除AAA级，CCC级（含）以下等级外，每一个信用等级可用“+”、“-”符号进行微调，表示略高或略低于本等级。

短期债券信用评级等级划分为四等六级，符号表示为A-1、A-2、A-3、B、C、D，如表5-2所示。

表5-2　短期债券信用评级等级划分表

注：每一个信用等级均不进行微调。

2.评级过程

评级机构通常对产品有严格的评级标准，会根据产品及发债公司状况提供严谨的评估结果，若掌握数据不足，评级机构将拒绝提供评级报告。国际评级机构多采用定性分析与定量分析相结合的方法进行评估，而在我国由于资产证券化业务刚刚起步，在评级过程方面学习国外的方法，并结合中国经济发展各阶段特点对评级产品进行测算。

图5-1　评级流程图

从图5-1可以看出评级过程一共分为八个步骤：首先评级机构与发行人召开会议，接着评级机构对发行产品进行定性、定量测算，再经由首席分析师提出建议，评级委员将综合各方面意见给出评级结果。若发行人不满评级机构的结果，可以提交补充材料并提出上诉，评级机构根据完整信息可以选择更改或者保留原评级结果，并向社会大众公布最终结果。发布结果并不是评级过程的终结，评级机构需持续观测发行人的业务与财务能力，若出现引起评级机构关注的因素并使发行人被加入到信用观察列表中，评级机构将在对发行人进行全方位分析后公布新评级或保持原有评级。

最后一步“展望”包含预测性质，积极的展望结果表示公司可能未来发展态势良好，偿债能力优异，反之则表明公司未来可能陷入财务困境。但预测并不一定精准，我们需要认识到评级机构给出的结果并非鼓励投资者购买某一类型的证券，不同评级的债券价格可能不同程度地被低估或者高估。

3.评级与违约率之间的联系

评级并不是对应着精准的违约率，不同的等级标明了不同的风险范围：评级高则风险相对较小，违约可能性较低；评级低风险相对高，违约概率也随之增大。表5-3显示了标准普尔每个评级类别不同期限的累积违约率，从表中我们可以看出，在相同的期限下，评级等级与违约率存在着反向变动的关系。这也表明，评级机构的评估结果是值得参考的。

表5-3　标准普尔全球受评发行人平均累计违约率（1981—2015）　单位：%

续表

数据来源：Standard ＆ Poor's Global Fixed Income Research and Standard ＆ Poor's CreditPro。

此外，发行人的信用评级变化会给投资者收益带来不可预测性，因此投资者还必须充分考虑信用评级转移的风险。信用等级转移是其了解、掌握金融市场违约风险变化的重要途径之一，对债务市场的各方参与者均具有重要的意义。

4.估计累计违约率和转移矩阵

1）转移矩阵及其稳定性

在金融框架下，评级机构会计算一个评级类别到另一个评级类别的转移概率，由不同评级的转移概率组成完整的信用等级转移矩阵（credit rating migration probability matrix），来反映债务人信用在不同信用等级间的变动，揭示债务人违约风险变化的趋势，其出发点就是通过了解（预测）未来每一段时间内一个金融机构所有可能的信用质量状况，从而进行有效的违约风险管理。矩阵各元素都是非负的，并且各行元素之和等于1，各元素用概率表示，在一定条件下是互相转移的，故又称为转移概率矩阵。这个概念首先于1987年由摩根公司提出，后来被标准普尔和穆迪公司采用。

信用转移概率矩阵是指一段时间内，信用等级从一个状态变为另外一个状态，由这种信用等级的迁移及其概率所形成的矩阵。当出现违约事件时，常常伴随着债务人盈利能力、财务状况、资本状况及流动性等因素恶化的现象，这些正是债务人偿付能力下降的标志。同时，债务人偿付能力的下降不是一步到位的，而是在违约之前已经经历了一个逐渐下降的过程，也就是信用等级的下降。于是，信用转移概率矩阵可以用来测算违约概率，体现违约风险的变化。

虽然转移矩阵提供的是事后信息，但是对于给定评级类别的违约概率，在惯性作用下，随着时间的稳定以及评级机构所使用标准的稳定，转移矩阵的使用将具有前瞻性。然而据相关文献显示，转移矩阵似乎与经济周期相关。例如，在经济衰退时期，评级下调次数和违约率都会上升。

2）估计累计违约率

（1）队列分析法

对评级公司而言，通常的方法是通过观测相同评级的公司组（即队列，cohort）的表现来求得历史平均违约或评级转移概率。这种风险管理可以减少经济周期和其他经济影响带来的波动，在长期“穿周期”风险管理背景下，队列分析法可以较好地减少不同经济周期所带来的影响。

以t时刻为例对所有公司开始分析。从t时刻来看，T年时的边际PD的估计值为。式中Nk（t）为第k个队列在时刻t的公司总数；Dk（t，T）为T时期内违约观测值总数。

取时间点t的M个不同的点的队列重复这一分析估计T时期内的无条件PD：

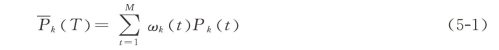
无条件累计PD主要使用两种计算方法。第一种方法将T时期内违约（边际）数Dk（T）替换为T时期内的累计违约数，该方法的缺陷是T期间内，一些评级由于公司的主动撤回而被转移至未评级分类，未评级分类的数据是无法获得的，在随后的分析中此类信息将被忽略。

另一种方法是从无条件边际概率来计算无条件累计概率，通过递推来避免信息的损失：

队列分析的主要缺陷是在过去未曾观测到违约的情况下，无法推导出非零概率。然而在实际情况下，即使概率非常小，高评级公司也的确存在违约概率。

（2）持续时间法

Lando和Skodeberg（2002）提出了通过久期技术来估计迁移概率，具体来说就是在一个持续时间（或风险）模型框架下计算，这一框架能够准确捕获转移的时间点，持续时间分析涉及一个马尔科夫链的生成元矩阵的估计。

将队列分析与持续时间法进行比较，在队列估计的框架下，假设评级转移满足一个时间齐次的马尔可夫过程。但该种假设，第一没有具体考虑到事件的时间t；第二在观测期T时期内，可能会发生多个不同的转移；第三由于t的选择和队列数量的选择的不同，观测值也可能会发生变动。相比较低效的队列分析，持续时间法使用久期技术法是在持续的时间框架下，对一个马尔可夫链的生成元矩阵进行估计。以下是两者的具体差别分析。

首先，在队列分析下，如果过去未观测到违约情况，在未来的持续时间下就无法推导出非零概率。尽管在实际中，对于高评级的公司来说几乎不可能观测到违约，但违约的可能性的确存在。

其次，队列分析可能会高估违约风险。在时间齐次下，估计马尔可夫链的生成元时，当公司从较低评级转向较高评级时，在该年份中公司会停留在较低评级一段时间，期间会取得一些较低评级的数据。相比较队列分析，这些变化使较低评级整个评级分类的分母增加，从而导致较低评级的违约强度减少，即违约概率变低。

最后，对于极端债券（CCC级）的违约概率，效率较低的队列分析与持续时间法相比，会明显低估极端债券的违约概率。原因大概是，在持续时间法中，公司只会花很少的时间在CCC评级债券中，会产生一个较小的分母，导致违约概率较高。

（二）统计方法评估累计违约率(www.xing528.com)

在分析违约风险时，投资者与机构需要对风险进行建模计量，通常会使用一些统计方法，用于对给定时间段的违约率进行建模与信用评分。它们有一个共同的特点，即债务人的评估数据是从过去的公司数据中学习获得的，而非导入与违约机制相关的因素。目前，使用较多的一些可用于建模PD或获得信用评分的统计方法是：逻辑回归和概率、最大似然估计、贝叶斯估计以及最小相对熵模型等。

1.违约率建模

违约率建模广泛地应用逻辑回归方法。逻辑回归方法是一种广义的线性回归分析模型，常用于数据挖掘、疾病自动诊断、经济预测等领域。逻辑回归的因变量为结果，例如违约就是“1”或“是”，非违约则为“0”或“否”，而自变量就可以包括很多风险因素。通过逻辑回归分析可以得到自变量的权重，从而可以大致了解哪些风险因素对违约有着重要影响。逻辑回归计算的给定条件X下的违约概率为

其中，X为风险因素向量，且X∈Rd；“1”表示违约；fj（X）为特征函数集，可以当作是泰勒展开的以X为自变量，能表明违约率与风险因素关系的可取函数，j=1，…，J；βj为参数。条件违约率是特征函数集的线性组合的逻辑变换。

假设特征函数为线性，则

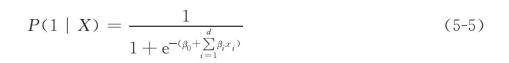
或者将特征函数设置所有风险因素一阶与二阶的组合，则

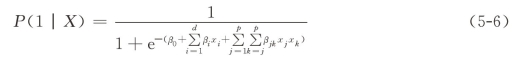
为了估计上述模型的参数β，我们可以采用最大似然法：

其中，（Xi，Yi）是一组风险因素和违约指标的观测值。

为了降低模型的过度拟合，我们可将模型正则化，即L（β）+R（β）。其中R（β）是正则形式，可以求出绝对值最大时的βj，得出的违约率会比最大似然估计得出的违约率更平缓。

2.违约率模型的分析

模型完成后，我们需要评估模型的有效性。一般信用评分模型评估指标大致可以分成两类：预测能力指标，用于评估模型对违约事件的预测能力；稳定性指标，用于评估模型在训练样本和测试样本中预测能力的一致性。具体方法采用基尼曲线、累计精度曲线（CAP）、受试者工作特征曲线（ROC）以及对数似然比率等对违约概率模型的计算结果进行评估。

1）基尼/CAP方法

此方法参照Hosmer and Lemeshow（2000）提出的基尼方法。经济学中的基尼系数是将一个国家所有的人口按最贫穷到最富有进行排列，随着人数的累计，这些人口所拥有的财富的比例也逐渐增加到100%，按这个方法得到图5-2中的曲线，称为洛伦兹（Lorenz）曲线。基尼系数就是图中曲线上与曲线下部面积的比例。可以看到，假如这个国家最富有的那群人占据了越多的财富，贫富差距越大，那么洛伦兹曲线就会越弯曲，基尼系数就越大。

同样的，假设100个公司的信用评分按照从高到低进行排序，以横轴为累计公司比例，纵轴作为违约概率，随着累计公司比例的上升，违约的比例也在上升。

图5-2　基尼系数

基尼系数的定义如下：给定n个有序个体的样本，其中xi是个体i的大小，将违约率按事件占比排序，并且x1＜x2＜…，＜xn，Lorenz曲线是为连接点的曲线。

其中，h=0，1，2，…，n，L0=0；

如果所有个体的大小相同，则

洛伦兹曲线为直线对角线，其中F（x）是累计分布函数，是μ为xi的平均值。

个体大小不均等时，可以用基尼系数来形容不均衡程度，基尼系数容易由无序大小数据计算成“相对平均差”：

或者，基尼系数的范围从最小值到理论最大值1排序时，基尼系数为

在信用体系中，基尼系数一般在50%～85%范围内。图5-3是信用基尼系数的示意图，假设将债务人按照违约可能性从高到低进行排序。理论上，若将D最高的违约率分配给实际上已经违约的N个公司，一个完美的模型会将是从点（0，0）到点（D/N，1），然后是从（D/N，1）到（1，1）的水平线。而一个无信息的模型会将不同违约率随机分配给不同风险的公司。得到的CAP曲线是从（0，0）到（1，1）的对角线（见图5-3）。

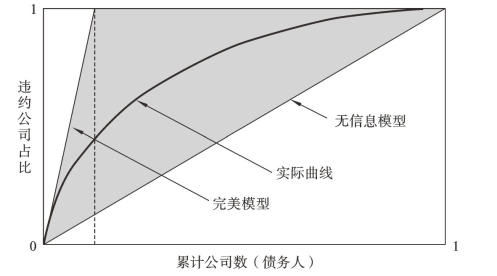
图5-3　信用体系基尼系数

实际的基尼评分模型都会在完美模型与无信息模型之间。如果这个评分的区分能力比较好，那么越大比例的违约会集中在越低的分数区间，整个图像形成一个凹下去的形状。所以洛伦兹曲线的弧度越大，基尼系数越大，这个模型区分好坏样本的能力就越强。

2）ROC方法

一种与基尼系数密切相关的方法就是ROC（Receiver Operating Characteristic）曲线法，又名“接受者操作特性曲线”。这里需要引入与机器学习有关的混淆矩阵（confusion matrix）内容。该分析超出了我们以往理解“正确率”的限制，使我们可以多维度评价一个模型的预测能力。

在使用一个模型去判断一个样本是“正样本”还是“负样本”的时候，模型会输出“正”或者“负”两种预测作为预测值；而实际样本会有正样本或者负样本两种情况，又为实际值。将预测值和实际值各自两种情况交叉组合就形成了表5-4所示的混淆矩阵。

表5-4　混淆矩阵

混淆矩阵衍生出以下几个重要的评价指标：准确率（AR）=（TP+TN）/N；召回率（TPR）=TP/（TP+FN），表示在所有实际是正样本中有多少被正确识别为正样本；误报率（FPR）=FP/（FP+TN），表示在所有实际为负样本中有多少被错误识别为正样本；查准率（PR）=TP/（TP+FP），表示被识别成正样本的样本中有多少是真的正样本。

采用ROC方法时，我们以混淆矩阵的FPR为横坐标，TPR为纵坐标。通过给定正、负样本分界线进行模型预测，得出各指标概率，并重复以上步骤，从而模拟出ROC曲线，而曲线下方的面积又名AUC（见图5-4）。

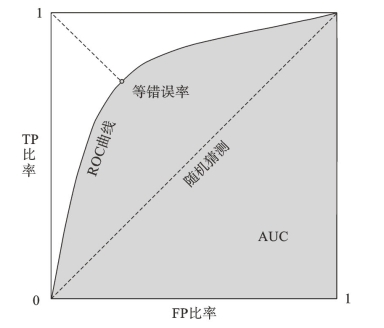
图5-4　ROC曲线

在ROC曲线下的面积与基尼系数之间存在简单的关系为：Gini=2（ROC-0.5）。

分析模型性能时，预测正、负样本的准确率越高越好，模型性能越强大，ROC曲线越接近（0，1）点，AUC面积也越接近1。在实践中，观察ROC曲线下面积大于0.9的情况极为罕见；反之，若该模型结果类似于随机猜测，那么ROC曲线就更接近于对角线，该个模型也将失去意义。

以上模型评价指标都限于将模型中的一组债务人违约率样本进行排序，忽略了违约率绝对水平的变化，若给定所有债务人违约率的绝对值发生相同变化，上述预测方法并不会随之改变度量结果。

3）对数似然比

在统计学家中最受欢迎的概率模型性能指标是对数似然比。此方法参照《结构金融学》（The Handbook Of Structured Finance，2007），为了测算两个违约率模型的相对性能，通常使用两个模型似然函数比的对数来进行估计：

其中（Xi，Yi），i=1，…，N，违约时为1，生存时为0。（Xi，Yi）为风险指标和违约率的观测对。

似然比检验也是为了检验模型好坏或者说是否恰当。似然比检验构造的似然比检验统计量，是比较全模型H1下极大似然估计和原模型H0下极大似然估计分别对应的似然函数。统计量比较大时，意味着H1极大似然估计的似然函数大于H0下的极大似然估计的似然函数，似然函数越大，未知情况越可能发生，相应的结果就越合理，这时应该不拒绝原假设H0。似然比法中两个似然函数值之比值λ只是样本观察值的函数，不包含任何未知参数。0≤λ≤1，因为似然函数值不会为负，且λ的分母为似然函数的极大值，不会小于分子。越接近H0时，λ越大；反之，与H0相差越大，λ越小。当λ≤λ0，拒绝H0，接受H1；当λ＞λ0，不拒绝H0。

基于上述原理，统计中广泛应用对数似然比检验，不仅计算方便，而且只要自由度大于1，就不必考虑理论频数大小的问题。