专项计划的现金流出及分配规则-《结构金融学》

负债侧现金流，即专项计划的现金流出，指按规定向不同层级投资者以及参与交易各方进行收益分配，由专项计划设计决定。一般情况下，当发生违约事件或加速清偿事件触发信用违约机制时，负债端现金流会改变其分配顺序，以保证优先级的投资者先得到偿付。分析负债端现金流主要应用的是瀑布模型，下面将详细介绍。

（一）摊还方式

过手摊还是指各档证券本金没有固定的兑付计划，根据基础资产的现金流回流的实际情况，在兑付日将收到的现金流全部进行分配。

违约率和早偿率的存在，给过手摊还证券的投资者带来了很大的不确定性。比如，如果早偿率提高，那么现金流就会变多、流入时间也更早，而过手摊还证券，本金是没有固定的兑付计划的，这就导致正常预计一年期兑付的证券，可能在7个月后，就完成了本金兑付——投资者有很高的再投资风险。而如果违约率升高，现金流回收就将低于预期，能够分配的资金就变少、变晚了，这就导致正常预计一年期兑付的证券，可能在1.5年后才完成本金兑付——这也是投资者不愿意看到的。

计划摊还是指各档证券本金有固定的兑付计划，投资者可以在约定的时间获得约定的现金流分配。

计划摊还对现金流进行了重构，本金摊还模式变成了固定摊还，持有这类证券的投资者，不用再担心现金流不确定的问题。但是，现金流的重构，只是解决了本金摊还模式的问题，并不能改变基础资产两个主要的风险特质：违约风险和早偿风险。因此，计划摊还也有副作用：假设违约率上升，对于一个过手摊还证券来说，也就是少一点、晚一点拿到本金而已，期限拉长一点，总能收回；而对于计划摊还来讲，这可就是原则问题，本来应该收到的钱没收到，就会触发证券评级下调，还有其他一系列风险缓释措施。

（二）负债模型的建立

这一节阐述了所有转付型结构中最简单的一种：原始交易。在原始交易中，信用增级唯一的方式就是息差和附属结构。原始交易是极为罕见的，因为很少有投资者仅仅依赖于当前可以收集到的信息进行投资，而对于预期外市场变动、信用风险或者是流动性短缺这类事情没有准备，这种情况下，如果发生违约等突发事件，证券持有者会显得措手不及。我们的目标不是模拟实际的交易，而是要尽可能地掌握基本的配置和付款数据。原始交易支付制度最常见的有：按优先顺序（sequential）和按初始比例（prorata）两种方式。而原始交易的公式基于两个债券A和B的完全抵押交易，债券上有具体每月的付款日期。负债模型参数的具体解释说明如表4-2所示，模型建立中涉及以下相关术语。

债券结构：一般来说，指的是结构化金融交易中的主要配置方法，或者是涉及自上而下类似瀑布原理的整套现金配置模式（不仅仅是本金），我们将在后面详细分析诸如保险单等特殊分配机制。

瀑布原理：规定了现金在SPE中如何分配给债券持有者，每一层瀑布都被视为一个级别，瀑布可能有任何数量的级别，下面的例子则是将其分为六个级别。

同等付款权利：在瀑布中的同一级别进行单独分配时，该级别的债券持有者被认为是平等的。

优先分配：首先将本金分配给高级别的债券持有者，其次为次级债券持有者，这种分配结构被称为优先分配。

初始比例分配：债券持有人的总本金按比例分配，如基于每个级别的初始本金余额，这种分配结构被称为按比例分配。

表4-2　模型参数的具体解释说明

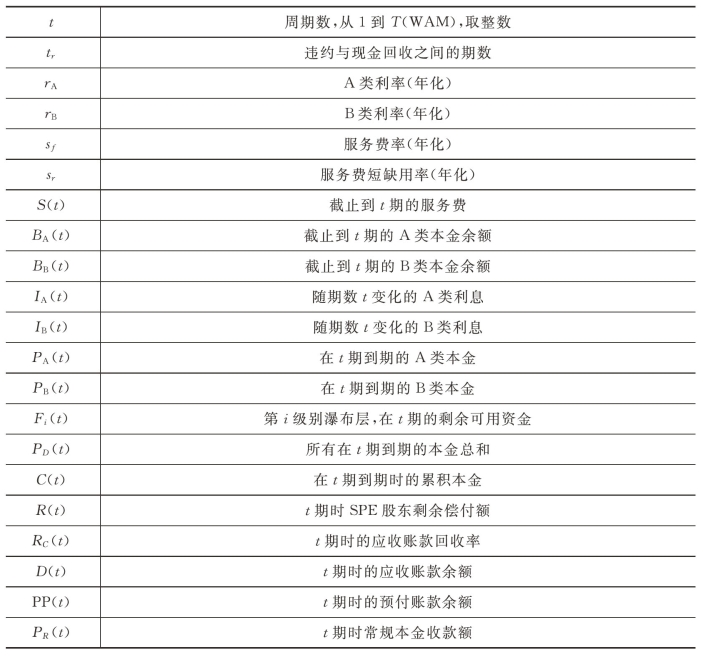
续表

下标P指支付的金额，最多等于总额；下标S指短缺的金额，最多等于总额。

例如，PAP（t）指A类本金支付金额，PAS（t）指A类本金短缺金额。这种标注适合所有的金额指标，且所有的金额指标都是非负的。在任何收款期间支付的所有金额的累计必须等于该收取期间的可用资金［F0（t）］。

放款率（advance rate）作为一项评估指标，指的是贷款人根据借款人的资产价值来评估借款人的贷款额度和信用额度。贷款人依据现有条款和资产市场价值考虑借款人还款的能力，再确定抵押品的市场经济价值之后，贷方会通知借方当前放款率和借款的最高限额，以尽量减少贷款人承担的风险。虽然放款率主要根据抵押资产的价值，但同时也会考虑借款人的财务信息。

（三）瀑布模型解析

瀑布原理（waterfall）由温斯顿·罗伊斯于1970年提出，最先被应用在软件开发模型上。瀑布模型将软件生命周期划分为制定计划、需求分析等自上而下且相互衔接的固定次序，就像瀑布流水一样，因而得名。在结构金融现金流的分析中，我们使用瀑布原理，根据资产证券化不同的优劣顺序，将贷款本息偿还次序划分为多个结构。

分级结构的每一层结构类似，均包括以下四个结构：应付金额、支付金额、短缺金额、剩余可用资金。而在原始瀑布（the raw deal waterfall）中，瀑布结构包括以下六个级别：服务及其他费用、A类的利息、B类的利息、A类的本金、B类的本金、剩余付款金额。额外资金来源，比如说储备账户和保险单，将作为额外的水平分级出现在瀑布中。关于剩余付款金额，它的应付余额总是等于支付余额，所以它的金额短缺一项，以及剩余可用资金一项均为零。

在任何时候，进入瀑布模型前均需要以下数据。

可用金额：F0（t）=P（t）+RC（t）+I（t）

应付本金总额：PD（t）=D（t）+PR（t）+PP（t）

启动A类余额：BA（t-1）

启动B类余额：BB（t-1）

累计应付本金总额：C（t）=PD（t）+C（t-1）

瀑布级别（waterfall levels）

1.服务及其他费用

应付服务费用：

支付服务费用：SP（t）=min（F0（t），S（t））

短缺服务费用：SS（t）=S（t）-SP（t）

剩余可用资金：F1（t）=F0（t）-SP（t）

2.A类的利息

A类的应付利息：

A类的支付利息：IAP（t）=min（F1（t），IA（t））

A类的利息短缺：IAS（t）=IA（t）-IAP（t）

剩余可用资金：F2（t）=F1（t）-IAP（t）

3.B类的利息

B类的应付利息：

B类的支付利息：IBP（t）=min（F2（t），IB（t））B类的利息短缺：IBS（t）=IB（t）-IBP（t）剩余可用资金：F3（t）=F2（t）-IBP（t）

4.A类的本金

A类的应付本金（按优先顺序分配）：

A类的应付本金（按初始比例分配）：

A类的支付本金：PAP（t）=min（F3（t），PA（t））

A类的本金短缺：PAS（t）=PA（t）-PAP（t）

A类的结束本金金额：BA（t）=BA（t-1）-PAP（t）

剩余可用资金：F4（t）=F3（t）-PAP（t）

5.B类的本金(www.xing528.com)

B类的应付本金（按优先顺序分配）：

B类的应付本金（按初始比例分配）：

B类的支付本金：PBP（t）=min（F4（t），PB（t））

B类的本金短缺：PBS（t）=PB（t）-PBP（t）

B类的结束本金金额：BB（t）=BB（t-1）-PBP（t）

剩余可用资金：F5（t）=F4（t）-PBP（t）

6.剩余付款金额

剩余应付金额：R（t）=F5（t）

剩余可用资金：F6（t）=F5（t）-R（t）=0

请注意，在这个简单的结构当中，最后一步很显然是多余的。第5级中的剩余可用金额总是等于第6级中的剩余应付金额。在我们的模型中，剩余现金金额属于卖方。在替代模型结构中（代数上等效），剩余现金流很有可能被认证（变成证券），并且保留在资产负债表上或者出售给第三方。其实，在这其中有很多复杂结构需要其他处理，例如，在第5级的剩余可用资金可以被资本化，并且在其他的分级付清（Z债券）之后到期，或者它们可以被分到若干个其他的分级。

（四）储备账户和流动性功能分析

种类不同的储备机制有很多不同的名称：储备金（reserve fund）、储备账户（reserve account）、现金账户（cash account）、抵押账户（collateral account）、息差账户（spread account）和收益率补充账户（yield supplement account）等。这里储备金是在交易中放置、持有和释放现金的一种机制。

在深入研究储备金的数学模型之前，有必要说明一下流动性和信贷手段之间的区别。流动性是指可用于付款的现金，特别是偿还时间迫切的情况，且违约的可能性比较小。当回报是可量化的但不高，并且承担风险的溢价不确定时，信用是债券持有人考虑的重要因素。在模型方面，流动性和信用增级之间的差异体现在偿还过程中在瀑布内占据的位置。交易模型中的层级结构可分为：服务或者其他费用、A类利息、B类利息、A类本金、B类本金、剩余金额。

要构建储备账户，需要通过在B类本金之下添加储蓄账户来修正瀑布，或者更通俗地讲，层级结构中最低级分类会受益于此，层级结构被修正为：服务或者其他费用、A类利息、B类利息、A类本金、B类本金、储备账户提取报销等。储备金是准备偿还除A、B外其他级别本金的，而这些级别又恰好受益于储备金。如果储备金中的资金被提取，这种结构只能在偿还完两个级别后再补充。无论如何，其当前余额按照合格投资率计算利息。

这种架构分析在逻辑上很准确，因为信用风险是本金的风险，储备账户位于本金分配之下。为了突出这一点，按照以下顺序考虑在瀑布中的账户：服务或者其他费用、A类利息、B类利息、设施提款报销、A类本金、B类本金、剩余金额。

由于提款偿还高于主要分配，该功能不提供信用增级，只是在现金不足以支付两类利息的时候，提供一定的流动性。在这个结构当中，任何现金必须首先分配于设施上，然后再用于A类和B类的摊销。在这种情况下，在交易中的储备账户提供的是流动性，而不是信用增级。除非设施位于本金的所在评级之上，否则它的形式意义不是流动性。事实上，一些现金池适用于这个结构不是它成为流动性储备的理由。

（五）准备金账户

在原始交易中，加入储备账户机制较为容易。一开始，在B类本金配置之后，令剩余资金F5（t）分配给持有人，我们使用它来满足储备账户的当前需求。模型符号含义如表4-3所示。

表4-3　模型符号含义表

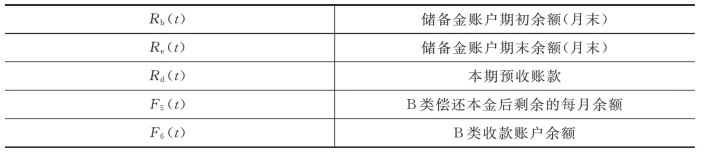
续表

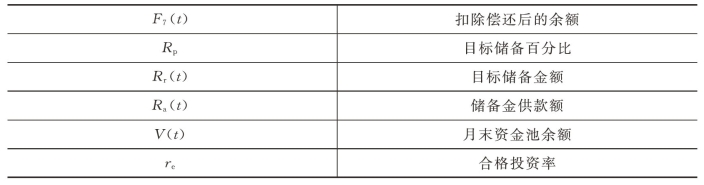
该功能应该能够偿还储备账户的资金，并且使用剩余现金收入，将其纳入目标百分比，从而帮助交易应对所有强制性付款。任何资金短缺必须由以后期间内所流入的现金支付。举例，研究在B级分配后的瀑布中输入以下公式：

账户Rb（t）将加入当前余额追踪，然后弥补可用资金。回想一下，在我们的基本模型中，可用资金值等于每个月的现金集合。如果可用资金足以支付目前i级的索赔，那么毋需追加储备金。在代数上，这种情况则是目前可用资金超过本期储备金的期初余额。差额等于本周期的剩余资金集合，逻辑上，这意味着：

当可用资金小于当前期初储备金余额时，差额等于收款的短缺额。如果可能的话，储备资金需要弥补这个短缺额。代数表达式：

对于动态储备，这个目标表示为当前资金池余额的百分比：

对于静态储备，这个目标表示为初期资金池余额的百分比：

储备金缴款将始终是目标余额和该水平下剩余现金中的最低额。注意，当达到目标余额时，储备量为负数，即现金从储备账户释放给发行方。

期末余额计算：

储备金账户充足时现金流计算如下：

一旦这些公式被应用到现金流模型中，由F7（t）表示的每月收集的资金，就会一样简单地流回卖方。

如果规定该功能提供流动性，而不是增强信用，我们将在瀑布较高级别插入相同的方程（如在B类利息到期之后）用以反映现金的预期用途。这将会导致结构特征表现为流动性设施。如上所述，在流动性和信贷设施在瀑布位置上的差异没有代数表现形式，但是它们的根本效用是不同的。最后，需知流动性设施的合格投资率为负数。

（六）基于压力测试的证券评级

结构化证券中存在的所有估值原理，都意味着反映或者忽略风险的某些关键维度的决策，包括时间、概率和分散性。前面建立的现金流模型，可以用于研究时间对价值的影响，但是每次研究只能设置一定的假设，模拟运行一种情况，如果该交易的所有差异都归结于这一种情况，即时间的检验，那么研究则不具备严谨性。

在现实中，我们不可能假定面对的真实市场只是模型中的一种，现金流运行的构建必须基于资产池，根据其所有可能的情况来设计。如何做到这一点是一个哲学问题：结果是基于滚动骰子（基于数据统计的视图）还是任意的解释呢（基于压力的视图）？在后一种情况下，压力情况决定了评级。标准普尔、惠誉在某些类型的交易中使用了这种方法。

基于压力的评级通过以串行方式施加压力来设计，从而发现被评估证券的安全性，所能够承受的最高负载，然后将这种压力评级分配给相应证券。当施加微弱的压力的时候，证券尚能够偿还，但是在更高压力之下违约，则将会得到较低的评级。可以承受相应比例外更高压力的证券将会得到更高的评价。

自20世纪70年代以来，穆迪的投资服务没有以压力测试方式定义结构化评级。相反，它以基于风险的数据统计视图来分配结构化评级，这需要通过蒙特卡洛模拟来探究信用损失分布以及其对负债支付的影响。在中国，压力测试流程和方法有着明确的规定，证券公司开展压力测试一般包括以下步骤：

（1）选择测试对象，制定测试方案；

（2）确定测试方法，设置测试情景；

（3）确定风险因素，收集测试数据；

（4）实施压力测试，分析报告测试结果；

（5）制定和执行应对措施。

虽然基于压力的评级方法易于处理，但是压力的校准工作比较困难，无法在不同交易之间评级在内部保持一致。此外，我们也不可能确保资产的类别、借款人的类型以及在不同地域的市场，因为每个环节都需要定制相应的压力。简而言之，基于压力的评级容易监测和逆向推导，但是基本不可能被验证。