结构金融学：资产侧现金流对底层资产池的质量和特征产生直接影响

资产侧现金流，即专项计划的现金流入，也就是底层资产池产生的现金流，主要由底层资产池的质量及特征决定，底层资产池的预期未来收益直接决定了该专项计划的预期未来现金流流入。

基础资产的预期收益主要由何种特征决定呢？这首先需要依靠基础资产的种类来判断，我们以目前ABS发行量规模增长最快的小额贷款资产类ABS为例来进行说明。我们将对基础资产现金流建立模型分为两个步骤：

第一步，不考虑风险，假设底层资产池内所有贷款都将按照合同约定按时还本付息，即无风险型现金流模型；

第二步，考虑逾期、坏账以及提前还款等风险事件，将早偿率、逾期率、违约后回收率、回收滞后期等因素纳入模型之中，即风险型现金流模型。

（一）无风险型现金流模型

如果所有贷款资产都按照合同约定按时还本付息，那么资产池产生的现金流是确定的，即在资产池形成之时，便可以得出其存续时间内具体的现金流。当然，无风险的资产池是不存在的，我们的讨论只是为了接下来便于理解风险型现金流模型。在无风险的假设前提下，决定现金流的因素有以下几点。

1.循环期与摊还期

当贷款资产的本息收回时，所收回现金流的去向可能有两种：一种是直接归集到专项计划账户之中，等待后续分配给投资者；另一种是再度投放将其贷给新的借款人，形成新的资产。而作为ABS基础资产的贷款资产池往往会设置循环期与摊还期，在循环期内，贷款资产产生的现金流再度投放形成新的资产，进一步扩大资产池；进入摊还期后，贷款资产的本息收入便直接归集到专项计划账户之中，不再进行新的贷款业务。

在循环期内，循环放款产生新的贷款资产，形成了子资产池，一般而言，子资产池需要单独分析，因为子资产池的借款人资质（信用记录）可能与原资产池不同，逾期率、早偿率等需要重新估计，贷款期限和利率也可能存在差异。当然，如果贷款资产完全同质，子资产池可以与原资产池合并分析。

循环期与摊还期的设置与ABS的整体设计以及负债端的收益分配计划相关，因为只有当基础资产池进入摊还期，专项计划账户内才会有现金流入，才可能进一步对投资者进行收益的分配。

2.摊还方式

摊还方式，是指借款人如何偿还本息，由还款频率、本金偿还计划等组成。目前市场上的摊还方式多种多样，如等额本息、等额本金、等本等息、先息后本以及到期一次还本付息等，下面我们对比较常见的还款方式做简单介绍。

等额本息，是指将收益和本息加起来后平均到每个月，每月偿还同等数额的资金，这种还款方式由于本金归还速度相对较慢，占用资金时间较长，还款总利息较相同期限的等额本金还款法高。

等额本金，是指在还款期内把贷款数总额等分，每月偿还同等数额的本金和剩余贷款在该月所产生的利息，这样每月的还款本金额固定，因而利息越来越少。借款人起初还款压力较大，但是随时间的推移每月还款数也越来越少。

先息后本，是指借款人在贷款到期日一次性归还贷款本金，利息按月归还。这种还款方式，一般适用于几个月的中短期借款项目。

等本等息，是指借款人每月偿还的本金和利息都是相等的，利息按照本金总额计算，再平均分配至各月。

一次还本付息，即贷款到期时一次支付所有本金和利息，中间不进行摊还。

摊还方式是决定现金流如何回款的重要因素，利率、期限相同的两种贷款，可能由于摊还方式上的差异，导致现金流完全不同。

3.利率

贷款利率毫无疑问是影响现金流的重要因素，它表示借款人进行贷款的价格，即需要按照贷款本金的多大比例支付利息。贷款的利率往往说的是年化利率，即贷款一年需要支付的利息与本金之比，对于整个同质贷款资产池来说，一般采用加权平均贷款利率。

4.期限

贷款期限也是影响现金流的基本因素，即一项贷款在何时应将所有应付本息偿还完毕。对于同质贷款资产池，我们一般采用加权平均贷款期限以及加权平均贷款剩余期限两个指标，因为ABS成立发行时间与贷款资产开始计息的基准日不一定相同。

5.未偿本金余额

截至某日的未偿本金余额，即基准日的未偿本金总额减去自基准日至该日期间所有已经偿还的本金数额。在计息日确定应付利息时，是以该日的未偿本金余额为基础，而不是按照本金总额计算。

（二）风险型现金流模型

相对于无风险模型的不切实际的假设，风险型现金流模型中将贷款逾期、违约以及提前还款等风险因素考虑进来，通过对逾期率、违约率及早偿率等进行假设来模拟贷款资产池的现金流。在建立模型之前，我们先对提前还款、逾期及违约可能带来的影响做一个简单的介绍。

1.提前还款

提前还款，主要是指借款人提前偿还贷款的行为。由于利率的波动，这样的行为通常会给证券投资人带来经济损失，我们定义这种投资风险为提前还贷风险。根据相关规定，借款人具备一定还款能力时，往往有权提前偿付部分或全部贷款，但是在这种情况下，贷款人提前还款的行为会影响证券持有人收到的偿付现金流。当提前还贷的速度过快时，后续偿付期间里面没有偿清的本金余额会变少，总体利息收益会相应减少；反之，当提前还贷的速度过慢时，那么偿付的时间就会比预计的时间更长，证券持有人获得资金的时间就会顺延变长，可能会错过更好的投资机会。

借款人是否提前还款往往与市场利率的变动趋向呈相反的态势。很明显，当市场利率下降的时候，借款人倾向于提前偿付，转而借入利率更低的贷款；而利率升高时，借款人倾向于滞后偿付，进而放慢还贷速度，更多地享受低息的好处。这就导致债券持有人在利率升高时，难以快速收回资金，而在利率走低时，又不情愿地收到大量廉价资金。计划摊还证券（Planned Amortization Class，PAC）是一种附加提前还款保护的债券，它可以在一定程度上对冲提前还款的风险。

PAC不同于“正规级”债券和“剩余级”债券，属于CMO各层级债券中比较特殊的一级。为了有效地对冲提前还款带来的损失，债券设计者将PAC的偿还优先级调至最高级别，其余所有CMO各层级债券均被称为“附属债券”，所有“附属债券”的摊还优先级低于PAC，但依旧遵循“正规级”债券和“剩余级”债券的偿还规定。设定的提前还款率边界不同，PAC对本金的吸纳水平也不同。当提前还款行为比较迅速时，PAC吸纳不了的本金将会分配至“附属债券”；当提前还款行为比较缓慢时，“附属债券”的摊还将会延迟而弥补PAC本金偿还的不足。简单来说，债券设计者将提前还款带来的现金流不确定性分摊至“附属债券”，用以维持PAC还款的稳定性。

2.贷款逾期及违约

贷款资产的违约一般指借款人未能按时偿还本息，造成贷款逾期或坏账，原因一般是借款人丧失还款能力或还款意愿。贷款违约对现金流的影响显而易见，不像提前还款那样复杂。

逾期率一般有几个指标来表示：M1逾期率表示逾期30天以内的贷款占贷款总数的比率，M2逾期率表示逾期31～60天的贷款占比，M3逾期率表示逾期61～90天的贷款占比，以此类推。而M3+表示逾期61天及以上的贷款占比，M2+表示逾期31天及以上的贷款占比，以此类推。

在静态的层面上，逾期率还可以用来阐述贷款违约后回收率，估算方法如下：用静态池中逾期91～120天的金额作为基数，然后看逾期151～180天金额数据。则1-（逾期151～180天金额/逾期91～120天金额）的数据就相当于逾期90天的贷款在60天内的回收率（因为逾期90天的贷款要么随后变成逾期150天以上，要么成功收回）。

3.预付款模型

1）条件提前偿付率

条件提前偿付率（Conditional Prepayment Rate，CPR），即是一种年化的提前偿付率，它等于每年提前偿付的金额占贷款池本金的比例。例如，若抵押贷款池的CPR为8%，则表明每年将偿付本金余额的8%。CPR越大，表明提前偿付速度越快；反之，表明提前偿付速度越慢。CPR的估计取决于很多因素，其中包括底层资产组合的性质、类似证券的历史提前偿付率以及当前和未来的经济环境。

CPR通常被定义为期间实际本金摊还T（t）减去计划本金摊还S（t），与期初资产总池平衡P（t-1）减去计划本金摊还S（t）的年度化比率，CPR公式如下：

然而，按揭付款每月都会发生，为了估计每个月的提前偿付情况，需要把CPR转换成月化的比率，一般称为每月提前偿付率（Single-monthly Mortality Rate，SMM），转换公式如下：

2）PSA模型

PSA模型以CPR模型为基础进一步发展而来，不同之处在于PSA模型并非采用一个单一不变的提前偿付率，而是一系列不断变化的提前偿付率，这更加符合现实情况，因为在现实中，刚刚办理抵押贷款的人不太可能提前还款。

PSA模型基本假设：成立时间越久的按揭贷款，其提前还贷的可能性越大；成立时间越短的按揭贷款，其提前还贷的可能性越小。但是，当贷款成立的时间超过30个月之后，其提前还贷的比率将稳定在一个恒定的数值，而不再变化。

这种假设的理由在于：第一，新借款人在支付了首付款之后往往会处在一个资金比较紧张的状态，不大可能在短期之内能够做出提前还款的行为；第二，新的贷款的利率水平往往更加接近市场水平，不太可能出现因为市场利率的大幅降低而促使借款人提前还款的情况。因此，我们可以这样描述PSA提前偿付基准比率：在贷款成立之后的首个还款期，即第一个月，贷款人的提前还贷比率为0.2%，其后每期逐月递增0.2%，依此类推，直到贷款成立的时间达30个月，此时的提前还贷比率为6%，从第31个月开始，数值保持在6%的水平恒定不变，直到贷款本息被全部还清。这一方法用标准模型，也称之为“100% PSA”表示。100% PSA模型提前还贷比率演变过程如图4-1所示。

通常用PSA的百分比数来表示提前还贷的各种可能性，即提前还款边界。比如：50% PSA表示是PSA基准提前偿付比率的，首期提前还贷比率为0.1%，以后每期逐月递增0.1%，直到第30个月达到3%，之后比率保持在3%直到本息还清。200% PSA表示是PSA基准提前偿付比率的2倍，首期提前还贷比率是0.4%，以后每期逐月递增0.4%，依此类推，直到第30个月达到12%，之后比率保持稳定直到本息还清（见图4-2）。

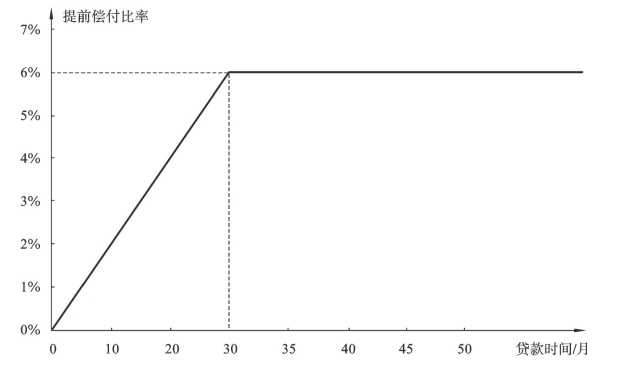
图4-1　100% PSA模型提前偿付比率

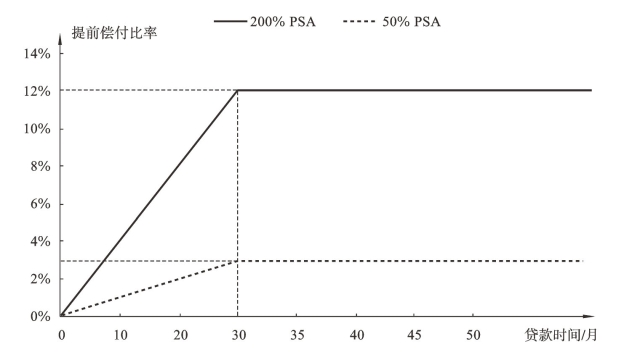
图4-2　50% PSA和200% PSA提前偿付比率

以PSA模型为基础的预测，初期被广泛地使用于结构金融市场，研究员通过模拟债券还款，用以预测债券的现金流水平。即使在初期，也因为现实市场的纷繁多样，PSA模型模拟债券预付款行为容易忽略很多现实因素，因此后来人们根据实际情况发展出了更为精确且复杂的模型。

4.风险型现金流模型

在考虑了提前还款之后，我们再将违约以及违约后回收加入模型，并进一步模拟这三者产生的预期本金损失，进而更加全面地模拟贷款资产池产生的现金流，真正建立起风险型现金流模型。风险型模型作为目前结构金融市场上较为有效的现金流预测模型，较好地模拟了现实市场中各种风险，模型使用更加广泛。

1）模型假设

风险型现金流模型基于无风险型现金流模型，能够更加精确地模拟原始资产池的各项参数，用以更好地描述资产池状态。为方便讨论，在模型中，时间t只取整数，即t∈［0，1，2，…，T］，另外，对风险型现金流模型做如下基础设定：

原始资产池中贷款数量：N（t），令N（0）≡N0

加权平均利率（定期）

加权平均期限（月）：WAM=T

实时资产池本金数额：V（t），令V（0）=V。

预期本金V0损失（%）为E（L）。

2）贷款状态

建立现金流模型是一个由浅入深的过程，模型从分析贷款整体的情况开始，进而分析由贷款产生的现金流。即根据资产池中各个贷款的状态，构建时间函数，并从贷款状态当中得到现金流量的大小。现金流量主要产生于借款人的还款活动，而借款人主要是以贷款账户来进行还款活动的，这使得贷款情况和现金流产生了很好的关联性。贷款有很多种不同的情况，主要可以被分为五种状态。

按时还款（performing as per the contractual schedule）：根据贷款时所签订的合同还款，其中时间表规定了还款时间以及金额。

全额预付（prepaying in full）：提前一次性还清所有贷款。

违约（defaulting）：违背贷款时所签订的合同。

部分预付（prepaying in part）：预付了大部分的贷款。

部分违约（partial defaulting）：在偿还过程当中，因某种原因已经不具有完全还款能力，但仍然偿还部分贷款。

3）风险型模型的预期损失估计

风险型现金流模型对预期现金流进行多方面的估计，其主要由损失曲线、累积分布函数、概率密度函数、账户空间等依次构成，尽可能全面地模拟现实结构金融的步骤。

（1）损失曲线

在开始构建信用损失模型之前，我们需要明白两个非常重要的点：第一，现金流建模的主要难点在于需要从违约行为所造成的资产池损失分布来判断债券的信用损失，即由损失分布来估计信用损失；第二，信用损失在这里指的是资产池本金的损失，而不是利息的损失（虽然损失本金意味着必然会损失一定的利息）。

我们还需要明确一个概念，损失曲线并不等于损失分布，即损失曲线不能和资产池的损失分布混淆。损失曲线是描绘单一资产池中累计损失的曲线，数据是可以被预测的。而最终随着贷款时间的推移，债券逐渐接近到期期限，预测值被发生损失的实际金额所取代，实际损失金额有可能与预测值一致，也有可能不一致。而累积分布函数（Cumulative Distribution Function，CDF）是在大量贷款样本库的基础上产生的所有可能的累计损失曲线的加总，它代表着资产整体损失的风险。

（2）累积分布函数

从数学角度出发，信用损失曲线的累积分布函数被定义为

从公式上可以直观地理解这个方程的含义，当t→∞时，分母趋于1，此时，F（t）逐渐趋于常数a。除此之外，我们分析其中的个别项数，当t＜t0时，指数值为负，当t＞t0时，指数值为正。我们可以很容易地看到边际损失曲线，即导数f（t）必须从零单调上升，在t=t0时达到最大值，在t＞t0之后单调减小。从现实角度来说，随着贷款时间的不断增长，资产池发生损失的风险会逐渐增大；但随着时间趋近于无穷大时，资产池整体损失的风险趋近于一个稳定的数值，不再发生变化，如图4-3所示。实际上，拐点lnb+t0的位置经常被选为“亏损清算比”（loss-to-liquidation ratio），定义为当前违约数额所占总资产的比例除以每月摊还金的比例。参数c确定拐点周围的曲线的斜率，c值越大，曲线越陡峭。最后，参数b决定了周期长度。我们适当地调整其四个参数，用公式（4-3）可以描述大多数资产池的信用损失行为。

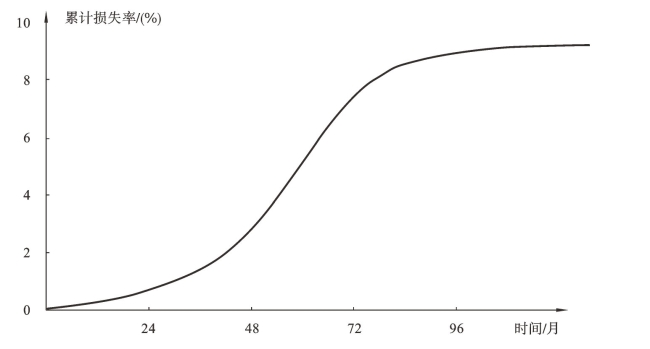
图4-3　信用损失的累积分布函数图

（3）概率密度函数

数学中，概率密度函数（PDF，Probability Density Function）定义为累积分布曲线的一阶导数，即dF（t）=f（t）dt。在“风险型”现金流预测模型中，我们用概率密度函数定义边际或每月损失，按百分比计算：

我们以月份为时间的基本单位，并将典型的参数值a、b、c、t0和T分别取值为：a=0.1，b=1，c=0.1，t0=55，T=120。将相应的参数值代入函数，得到图4-4所示的边际损失曲线。(www.xing528.com)

图4-4　边际损失曲线

（4）账户空间

账户空间L（t）不等同于实际资产池的金额，同样，违约账户所占的比例不总是等于违约现金所占的比例。在风险型现金流模型中，我们将违约账户空间与违约金额分开进行分析。举个例子，当资产池中的账户发生违约行为，且这些违约的发生集中在具有较高余额的账户中，那么由于存在等效性原则，可能会导致对资产池本金损失的估计不足，从而低估了损失的金额。为解决这一问题，我们将累计违约账户比例与累计违约现金所占的比例相乘得到损失曲线。然而，这样得出的仅仅是违约金额，而非损失金额，因为没有考虑违约账户的回收金额。

首先我们预测违约的账户在原始资产池当中的比例F（t），然后通过F（t）乘以原始资产池中的贷款数量N（0），以此将我们的结果映射到账户空间L（t）上。例如，假设初始资产池包含2000个贷款账户，我们模拟一个10%的预期账户损失，那么在整个时间期限内（即120个月），随着时间的推移，会有200个账户按照公式（4-3）的模式进行违约。

（5）归一化损失曲线

根据公式（4-3），只有当t无限趋近于正无穷大时，预期损失E（L）才能达到10%，然而贷款是有期限的，因此，按照逻辑曲线推算，E（L）永远不会真正达到10%，这与现实不符。所以，损失曲线通常需进行归一化处理，以便正确反映资产池的预期损失。为了纠正边际损失曲线和累计损失曲线的误差，需要标准化每个月的相关变量。

定义L（t）为累计非标准账户空间损失曲线（cumulative non-normalized accountspace loss curve），l（t）为t时刻边际非标准账户空间损失，nD（t）为t时刻边际标准累计账户空间违约率，N0为账户的初始数量，Dr为累计账户空间违约率，将预期损失定义为：E（L）=N0 Dr。

将F（t）转换为L（t）：L（t）=F（t）N（0）。

将L（t）转换为l（t）：l（t）=L（t）-L（t-1），假设T为累积违约的t的集合。

将公式归一化：

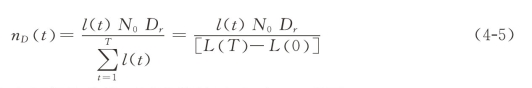
根据公式（4-5）得出空间损失曲线不同取值结果，如表4-1所示。

表4-1　空间损失曲线不同取值结果

（6）提前还款

虽然本章对预付还款做了一定的解释，但是在实际贷款中，真正的提前还款行为非常复杂。在结构金融中有很多变量对提前还款水平有较大的影响，其中最为重要的是当前的利率环境。目前，市场上存在很多可靠的预付款模型，但基本上都是有条件的预付款模型，即设定一定的已知条件。如果假设利率已知，相应的预付款利率就能够被准确地确定。当然，假设利率已知实际上就是忽视了主要问题。其实，除了RMBS，预付款都属于次级信贷的问题，因为只有少数借款人会因为利率的变动而改变自己预付的方式。在绝大多数ABS资产类别的短期资产池中，预付款行为的变化主要是因为利率以外的因素，而这些都是不能够预测的。下面提供的预付款公式具有PSA曲线的功能形式，但是作为初始资金的函数，这个特定的假设规定，在10年交易的整个周期当中，20%初始资金将会在其中某个时间点预先偿付。

边际预付款函数的每月账户空间提前还款率g（t）从0开始线性上升，直到其达到稳态t0p。我们将使用累计预付曲线G（t）计算每月账户空间的预付：

同时，我们定义G（t）为

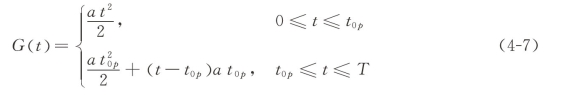
在这里，参数a在边际预付曲线中是0到t0p的直线斜率，假设t0p=48，可画出如图4-5所示的边际预付率曲线和图4-6的累计预付率曲线。

这里参数a是图4-5中0到t0p斜线的斜率。为了标准化这个贷款空间累计函数，令t=T，则以下的账户空间边界条件成立：

通过求解方程得到斜率a：

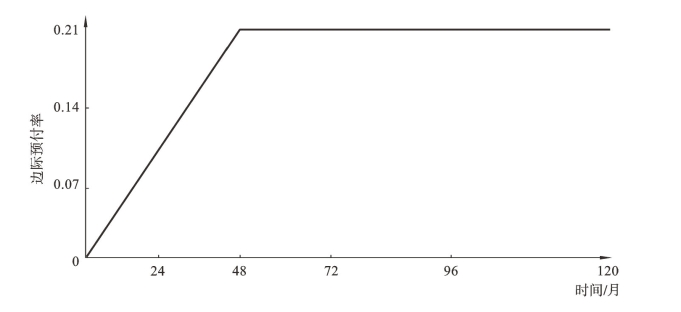
图4-5　边际预付率曲线

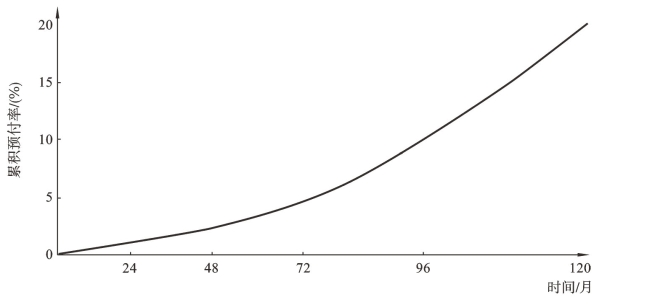
图4-6　累计预付率曲线

注意G（t）与参数a的线性关系。基于此就可以计算具有违约和预付款特征的资金池的现金流量。

5.资产现金流

1）贷款

假设资产池中包括N0个贷款，期间利率均为r，期限为T月，B（t）是随时间变化的本金余额，定义B0=B（0），贷款由以下一阶线性微分方程定义：

M为每期还款的金额，是一个常数，上述方程是可解的。方程当中的负号表示随着时间的增加，贷款的本金金额会减少。以下方程描述了同样的周期过程现象，但是能够更好地描述模型中的现金流。

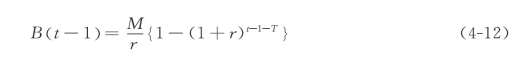
令两个边界条件B（0）=B0和B（T）=0：

在后续的章节当中，我们用方程（4-11）和方程（4-12）的表达式将每个月的付款划分为利息和本金现金流量。

2）期末贷款余额

每月月末，贷款余额定义如下：

3）利率

用公式（4-11）与（4-12）计算利率，令I（t）=［N（t-1）-nD（t）］rB（t-1），则

方程右边的是活期账户数和利率的乘积，左边是贷款账户数额，N（t-1）是（t-1）期末尚未偿还贷款的数额，nD（t）是本期间偿还的贷款数量。

4）本金

每个月收到的本金包括常规本金金额PR（t）和预付金额PP（t）。常规本金金额由每月固定摊销，利用方程（4-11）与（4-12）计算得到，其中大括号中的部分表示账户余额摊销的折现因子变化：

预付金额等于预付贷款的个数乘以t时刻的期末余额，因为每月摊销额度已经通过上面式子得到，因此我们首先使用余额来计算预付款：

则该时期的总本金金额为

5）违约

违约金额D（t）等于违约贷款的数额乘以在t-1时间点的尚未偿还的本金金额：

6）违约损失率

违约金额通常受回收金额RC（t）影响，比如抵押品在延期tr后被出售或者拍卖，而收益将通过信托机构来返还，那么

在上式（4-20）中，LGD（t-tr）是账户违约时，违约损失金额占本金金额的百分比，而t-tr中tr代表回收所需的延期时间。除此之外，违约损失率（LGD，Loss Given Default）的值与时间相关，因为回收的价值取决于二级市场中抵押品的公允价值和未偿还的本金余额。图4-7为典型的贷款摊销曲线与资产折旧曲线，表明了它们与时间之间的关系。

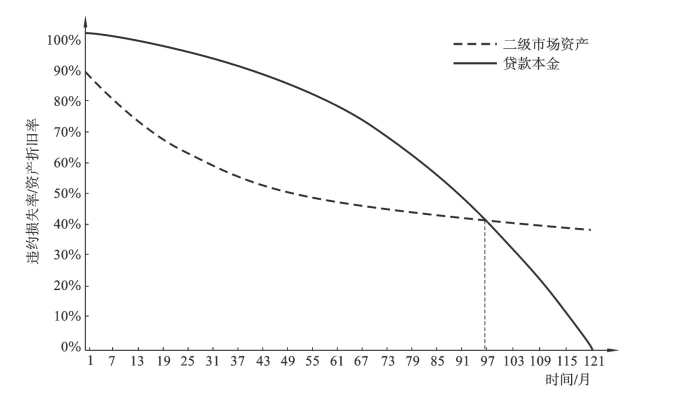
图4-7　损失摊销/折旧曲线

在t=0处的LGD是相关资产的零售值和批发值的差额，数额较小，之后差额单调增长直到t=40，随后在区间40到120单调减少，在96≤t≤120区间LGD＜0。

而由图4-7可以看出，在中间时段，回收金额占未偿还本金余额的比例往往是最小的，因为贷款的本金余额与抵押资产的折旧价值之间的差额在此处是最大的。相反地，在两条曲线相交时（t=96左右），理论上回收率为100%，因为资产价值等于未偿贷款余额。过了这点之后，信用利润将取代信用损失。虽然大多数法规不允许贷款人从这其中赚钱，但是在还没有违约的情况下，如果时间t已经到96，比较精明的债务人很可能不会违约，因为他们可以在公开市场上卖出资产，通过这种手段，可以全额偿还贷款余额。但是在现实生活中，很少有债务人如此聪明，可以如此巧妙地管理资产，因此在信用损失理论上为负的时候仍会出现违约。

为了构建基础的现金流模型，我们通常忽略二级市场中使LGD与时间相关的经济行为，假设所有人获得信息一致，LGD是一个已知的常数。

7）可获资金

从现金流的部分，我们可以计算每期的可获得资金AF0（t）：

其中P（t）表示本金的收回，是PP（t）与PR（t）之和。

8）到期本金

每个回收期，到期本金可以使债券持有人保留全部抵押：

显然，实际上只有前两项可以收回，而违约金额必须由超额利差所覆盖。

从负债端计算C（t），累计到期本金。作为总的到期本金：

9）期末本金池

在t时刻的期末本金池等于在t时刻最初资金池的基础上对月度摊销做一些调整。例如，减去计划本金支付，提前偿付与违约：

10）其他资产现金流

除了上述现金流之外，资产侧还有其他可能存在的现金流来源，比如储备金账户、保险政策等，本章不再做详细讨论。