1.观点。
建构主义是认知主义的进一步发展，是一种关于知识和学习的理论。强调学习者的主动性，认为学习是学习者基于原有的知识经验生成意义、建构理解的过程，而这一过程常常是在社会文化互动（同化与顺应）中完成的。
2.数学概念学习的APOS理论（以美国杜宾斯基（E·Dubinsky）为代表）。
（1）操作（活动）阶段（Action）：学生通过一系列外显的指令去改变数学对象的过程，它是获得数学概念的一个必要条件。许多概念的本质是内隐的，需要经过一系列外显的探究活动来获得，这些活动不仅仅是指学生的肢体动作，而是泛指所有的数学活动，如猜想、回忆、计算、推理等。
（2）过程阶段（Process）：当“活动”经过多次重复而被个体所熟悉后，物理操作就可以内化为“过程”的心理操作。有了这一程序，个体就可以想象之前的活动，而不必通过外部刺激和具体操作，甚至可以在脑中实施这一程序的逆转或与其他程序进行组合。
（3）对象阶段（Object）：当个体能将“过程”作为一个整体进行操作和转换时，这个过程就变成了他的一种心理对象。这时，个体可以操控对象去实施各种相关的数学运算。需要时，也可以具体再现对象所包含的过程步骤。
（4）概型（图式）阶段（Scheme）：个体对“活动”“过程”“对象”及其原有的相关图式进行相应的整合、精致，就会产生出新的图式结构（认知框架），从而可运用于问题解决情境。
【项目设计】试题（国家教师资格证考试·数学学科知识与教学能力（高级中学）模拟试题）：请以人教A版普通高中《数学》（必修，第一册）《函数的奇偶性》为例，用APOS理论设计其教学流程。
解析：
Ⅰ活动阶段
展示学生熟悉的二次函数f（x）＝x2和分段函数
，让学生作出图象，从图象上获得“对称”的感性认识。
Ⅱ过程阶段
（1）针对二次函数f（x）＝x2给出表格：
要求学生结合上面的表格，用数学语言（符号）描述图象的“对称性”。
（2）用同样的方法，分析分段函数
。(www.xing528.com)
Ⅲ对象阶段
（1）讨论上述两个函数的共性，总结归纳得出偶函数的形式化定义：若∀x∈I，都有－x∈I，且f（－x）＝f（x），则称y＝f（x）为偶函数。
（2）以一次函数f（x）＝x和反比例函数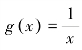
为例，类比得出奇函数的形式化定义。
（3）要求学生列举几个奇偶函数的例子，分析得到它们的图象特征：y＝f（x）为偶函数⇔图象关于y轴对称；y＝f（x）为奇函数⇔图象关于原点对称。
Ⅳ概型阶段
（1）题组一（代数运算）：判断下列函数的奇偶性。
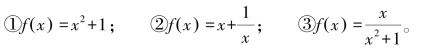
变式：如果f（x）＝x3＋b是奇函数，求实数b的值。
小结：
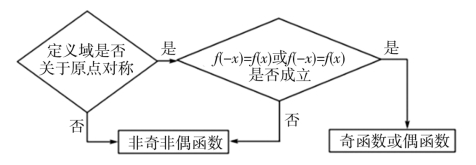
图5－2 函数奇偶性的判定
（2）题组二（几何直观）：已知f（x）是偶函数，g（x）是奇函数。试将下图补充完整。
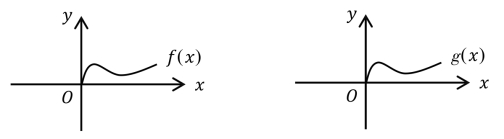
图5－3
（3）题组三（获取新知）：已知函数f（x）是偶函数，且在（0，＋∞）上单调递减，判断f（x）在（－∞，0）上的单调性，并证明你的结论。
变式：若将f（x）改为奇函数呢？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
