中学数学课程与教学新论-教学模式的发展、导学、质疑和检测

1.教学模式的理论基础进一步加强。

2.教学模式由“以教师为中心”，逐步转向更多的“学生参与”。

3.现代教育技术成为改变传统教学模式的一个突破口。

4.教学模式由单一化走向多样化和综合化。

5.探究和发现的数学教学模式将会有更大的发展。

【简介一】江忠东“六环互动”课堂教学策略。

第一环节是“导学”，即创设情境，促进学生自学。

第二环节是“精讲”，即启发讲解，促进学生自悟。

第三环节是“讨论”，即合作探究，促进学生自研。

第四环节是“展示”，即展示成果，促进学生自结。

第五环节是“质疑”，即互动研讨，促进学生自疑。

第六环节是“检测”，即随堂检测，促进学生自省。

（注：这六个环节，可以根据具体情况，在实际教学中微调顺序或作适当删减）

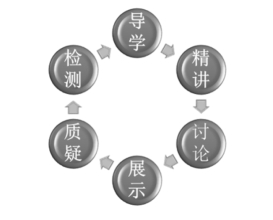
图4－17　江忠东“六环互动”课堂教学策略结构图

【案例分析】《简单复合函数的导数》。

Ⅰ导学

第一环节是“导学”，即课前提供阅读材料和问题情境，诱发学生唤醒旧知的意识和获取新知的欲望。

表4－8　导学案

(www.xing528.com)

Ⅱ精讲

（1）复合函数的导数运算法则：

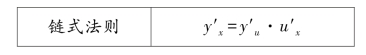
注：“小云的困惑”是她在求[g－1（x）]′时，误将复合函数g－1（x）当成了简单的幂函数。

（2）求下列函数的导数：

①y＝(2x＋3)2；②y＝ex－1；③y＝ln(x＋2)；④y＝sin(πx＋φ)。

解：①y′＝2（2x＋3）·（2x＋3）′＝4（2x＋3）＝8x＋12。

（本题可以先展开y＝4x2＋12x＋9，再求导。）

②y′＝ex－1·(x－1)′＝ex－1。

（本题可以先化简为，再求导。）

教师质疑：你能指出函数的单调性吗？其单调性与导数在相应区间上的正负有何关系？这种对应关系是否具有一般性？（为下节课学习作铺垫）

学生质疑：如果将题目改为“求过点（0，0）的正弦型曲线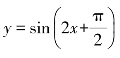的切线方程”，那么如何解答？（生成新知）

学生质疑：求函数y＝（3x－5）8导数，可否先用二项式定理展开，再求导？（拓展课堂）

Ⅵ检测

【简介二】成都市龙泉驿区的DJP（即“导”“讲”“评”）模式：

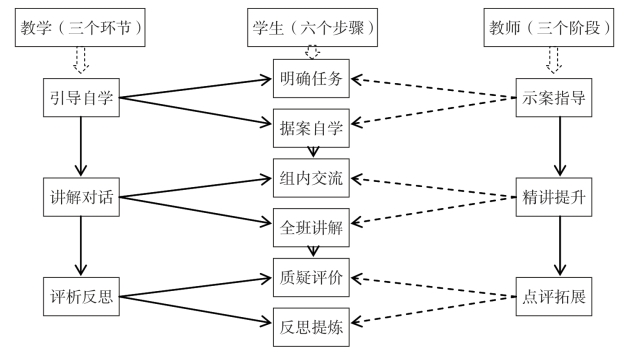
图4－18　DJP数学课堂教学基本模式