活动式教学流程特点、勾股定理应用

1.操作程序。

图4－10　“活动式”教学流程

2.模式特点。

（1）注重直观性；（2）激发主动性；（3）容易忽略活动本身蕴涵的数学内容。

【案例分析】《数学史话——有多大？》（人教版七年级下册）

Ⅰ探究新知

活动一：在坐标纸上画一个两条直角边分别为3和4厘米的直角三角形，然后用直尺测量斜边长。提出猜想：设直角三角形两直角边分别为a和b，斜边为c，则a2＋b2＝c2（勾股定理）。验证猜想：让学生作图验证。

（1）作一个两条直角边分别为6和8厘米的直角三角形，验证斜边长。

（2）作三边长分别为5、12、13的三角形，先计算三边平方关系，再测量大边所对角。

（3）量一量自己的直角三角板的三边长，看其是否满足勾股定理。

（4）算一算两直角边长为1分米的等腰直角三角形教具的斜边长。（分米）

Ⅱ运用新知

活动二：你能估计的大小吗？它在一个什么范围内（越精确越好）？

（1）借助计算器探索的整数部分是几？十分位是几？百分位是几？千分位呢……

（2）展示一个学生的结果，让其他人对比整理自己的结果。（不足近似值与过剩近似值）

（3）你能用平方关系验算所得结果吗？通过验算你发现了什么？

（4）如果用计算器计算，结果如何？（你可能会大吃一惊！）(www.xing528.com)

活动三：你能在数轴上找到表示的点吗？画一画，说说你的方法。

请大家把事先准备好的两个边长为1分米的正方形拿出来，以小组为单位，分别沿着它们的一条对角线剪开，得到四个等腰直角三角形，然后把它们拼成一个大正方形，想一想，这个大正方形的面积是多少？边长是多少？

请大家根据实验结果，在数轴上画出表示的点。

图4－11　数轴上表示

Ⅲ交流评价

活动四：怎样在数轴上作表示和－的点。

图4－12　数轴上表示和－

（1）在图4－12中的数轴上，以0—1的单位长度为边作一个正方形ABCD，连结AC，由勾股定理可得

于是，以点A为圆心，AC的长为半径作弧，在数轴原点右侧截得点M，则有OM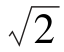＝，点M即为表示的点。

（2）在图4－12中的数轴上，以0—2的2个单位长度为边作一个直角三角形AEF，使∠AEF＝90°，且EF的长为1个单位长度，此时由勾股定理可得

于是，以点A为圆心，AF的长为半径作弧，在数轴原点左侧截得点N，则有ON＝－，点N即为表示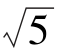－的点。

Ⅳ巩固提升

在数轴上画出表示和的点。

问：通过作图，你能得出一个什么结论？（每个实数都可用数轴上的一个点来表示）