学会用数学的观点考察现实世界，用数学的方法解决现实问题。
【案例一】某班有60名同学，请问是各人生日互不相同的可能性大，还是至少有两人生日相同的可能性大？为什么？
解析：设班上有n个人（n≤365），则
P（n个人生日互不相同）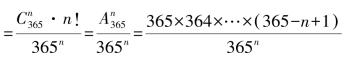
由此可得下列统计表（对立事件的概率）：
表4－1 n个人中至少两人生日相同的概率统计表
可见，50人左右几乎有两人生日相同。故该班至少有两人生日相同的可能性大。
包括符号化、逻辑化和公理化三个层面。
【案例二】概率的公理化定义：设E是一个随机试验，Ω为其样本空间，以E中所有随机事件组成的集合为定义域（事件域），定义一个函数P（A），若P（A）满足以下三条公理，则称函数P（A）为事件A的概率。
（1）公理1：非负性，即0≤P（A）≤1；
（2）公理2：规范性，即P（Ω）＝1；
（3）公理3：可列可加性，即若AiAj＝φ（i≠j），则
3.问题驱动性原则。（〔美国〕哈尔莫斯）
问题是数学的心脏。
【说明】数学学习的心理过程是一个“学——思——疑——问”的过程。《义务教育数学课程标准（2011年版）》把“初步学会从数学角度提出问题、理解问题，并能综合运用所学知识解决问题，发展应用意识”列为具体目标。为此，在数学中，应营造宽松和谐的问题环境，鼓励学生“敢问”；精心创设问题情境，促使学生“想问”；教会思维方法和提问技能，培养学生“善问”。
4.渗透思想原则。（中国数学教学特色）
七大数学思想：函数与方程思想，数形结合思想，分类与整合思想，化归与转化思想，特殊与一般思想，有限与无限思想，或然与必然思想。
【项目设计】（国家教师资格证考试·数学学科知识与教学能力（高级中学）模拟试题）分别用代数和几何的方法证明不等式链：(www.xing528.com)
若a，b∈R＋，则
当且仅当a＝b时取“＝”。
解析：
（1）代数证明
设a＞b＞0，对b，a作定比分点
易证函数f（x）在0[，＋∞）是增函数。
易知，当且仅当a＝b时可取“＝”。
（2）几何解释
如图，AB是圆O的直径，点C是AB上一点，AC＝a，BC＝b，过点C作CD垂直于AB，交圆O于点D，连接AD，BD，OD，过点C作CE垂直OD于E，以O为圆心、OC为半径画小圆，过O作OD的垂线，交小圆于F，连接OF，则
动态改变点C的位置，由DE≤CD≤OD≤DF，可得
当且仅当a＝b时可取“＝”。
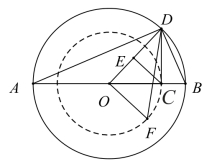
图4－3 不等式链的几何解释
5.整体设计原则。
教学必须在课程标准的框架下，以系统思维为指导，以单元教学为模块，围绕目标，统揽全局。
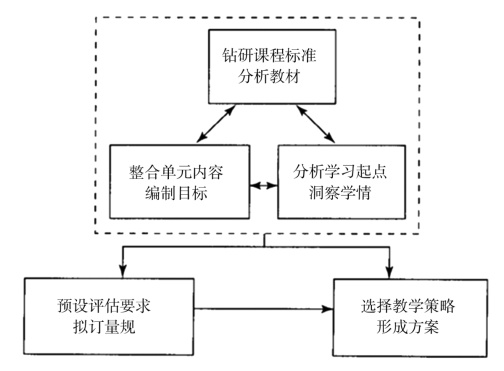
图4－4 单元整体教学设计的基本步骤
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
