1.教学观摩:观摩初中数学《解二元一次方程组》(人教版七年级下册)。
视频:“一师一优课,一课一名师”优课《解二元一次方程组》(宁波市东恩中学李珊珊)。
要求:从知识讲解、解题策略、组织形式等方面观察我国中学数学课堂的主要特征。
2.理论研讨:我国数学课堂教学的主要特征。
(1)“新知导入”(情境创设,启迪思维)。
【常用方法】新旧联系;情境创设;设疑悬思;趣味诱导。
【基本原则】针对性原则——突出一个“入”字;启发性原则——突出一个“导”字;趣味性原则——突出一个“趣”字;新颖性原则——突出一个“巧”字;直观性原则——突出一个“形”字;系统性原则——突出一个“联”字;简洁性原则——突出一个“精”字。
【案例一】初中数学拓展课《切割线定理》的情境导入。
《登鹳雀楼》中千古名句“欲穷千里目,更上一层楼”,反映的是诗人的写实风格,还是浪漫情怀?学完本节课,大家就能回答这个问题了。

图3-13
【案例二】人教版七年级下册《数学》中《平面直角坐标系》的设疑导入。
你能否以电话的方式,用一句话(单句)向远方的同学精准描述右图的形状?
(2)“尝试教学”(学生中心,自主探究)。
【成功经验】(上海)顾泠沅领导的“青浦经验”:尝试指导,效果回授;(江苏)邱学华倡导的“尝试教学法”:先试后导,先练后讲;(重庆)陈重穆领导的“GX教学实验”:先做后说,师生共作。
(3)“师班互动”(合作交流,适合国情)。
【主要方式】双向型:师生问答;多向型:小组合作;网状型:交互学习。
(4)“变式练习”(举一反三,触类旁通)。
【基本策略】一题多问;一题多变;一题多解;多题一解。
(5)“四基教学”(夯实基础,促进创新)。
【“四基”解读】“基础知识”是指数学课程标准所规定的基本概念、基本性质、基本法则、基本公式、基本定理等;“基本技能”是指在某种操作规则或者操作程序下通过实践、练习等方式掌握的操作技术和运用数学知识解决问题的能力,包括运算、测量、绘图以及问题解决等;“基本思想”主要是指数学抽象(如分类讨论、数形结合等)、数学推理(如化归转化、演绎证明等)、数学模型(如函数方程、统计概率等)等思想;“基本活动经验”与过程性目标相联系,“是一种从感性向理性飞跃时形成的认识”(张奠宙),“是学习主体通过亲身经历数学活动过程中获得的具有个性特征的经验”(史宁中)。
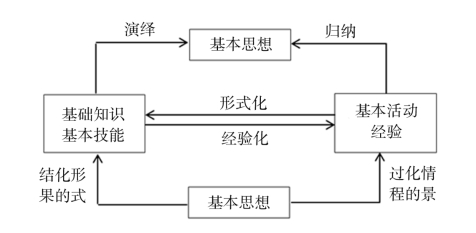
图3-14 四基结构图
【简介一】
“四能”:发现和提出问题的能力,分析和解决问题的能力。(https://www.xing528.com)
“三会”:会用数学眼光观察世界,会用数学语言表达世界,会用数学思维思考世界。
数学六大核心素养:数学抽象(数学的眼光)、逻辑推理(数学的思维)、数学建模(数学的语言)、直观想象、数学运算、数据分析。其中,前三项是数学基本思想,后三项是传统数学能力。
【简介二】高考数学素养与数学核心素养的关系

图3-15 高考数学素养与数学核心素养的关系
3.拓展延伸:数学课堂主要特征与数学教育基本理念的对应关系。

图3-16 中国数学课堂教学理念与课堂主要特征的对应关系
4.项目设计:变式练习的微课设计。
(1)项目设计。
请以人教A版普通高中《数学》(选择性必修,第二册)中“数列通项公式的求法”为例,进行变式练习微课设计。
(2)策略模型。
例题:若a1=2,an+1=2an-1(n∈N*),求数列{an}的通项公式。
一般性推广:递推式为an+1=pan+q(p≠1,p,q≠0)。(模型法,p=1或q=0时公式法)
变式1:若数列{an}中,a1=1,an+1=an+2n(n∈N*),求an。(累差法)
一般性推广:递推式为an+1=an+f(n)(n∈N*)。
变式2:已知数列{an}中,a1=1,an+1=2nan(n∈N*),求an。(累乘法)
一般性推广:递推式为an+1=an·f(n)(n∈N*)。
变式3:已知数列{an}中,a1=1,an+1=2an+2n(n∈N*),求an。(转化法、数归法)
变式4:设数列{an}的前n项和Sn满足Sn=2an-1(n∈N*),求an。(公式法)
变式5:设数列{an}满足a1+a2+…+an=2an-1(n∈N*),求an。(公式法)
文献阅读推荐:
[1]〔德〕克莱因著.舒湘芹等译.高观点下的初等数学(第三卷)[M].上海:复旦大学出版社,2008.
[2]张奠宙,于波.数学教育的“中国道路”[M].上海:上海教育出版社,2013.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




