波利亚解题理论在中学数学教学中的应用

1.“怎样解题”表。

为了回答“一个好的解法是如何想出来的”这一问题，波利亚专门研究了解题的思维过程，在《怎样解题》一书中，他分解解题的思维过程得到“怎样解题”表。以下是“怎样解题”表的简表。

表3－1　波利亚“怎样解题”表的简表

【案例分析】给定正四棱台的高为h，上底的边长为a和下底的边长为b，求正四棱台的体积F。（学生已经学过棱柱、棱锥的体积）

【解析】第一，了解问题。

问题1：你要求解的是什么？

要求解的是几何体的体积，在思维中的位置用一个单点F象征性地表示出来（图3－6）。

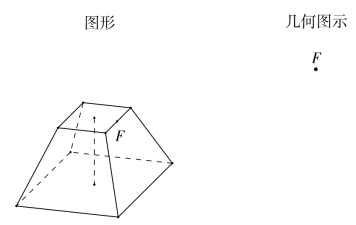
图3－6

问题2：你有些什么？

一方面是题目条件中给出的三个已知量a，b，h；另一方面是已学过的棱柱、棱锥的体积公式，并积累有求体积公式的初步经验。把已知的三个量添到图示处（图3－7），就得到新添的三个点a，b，h；它们与F之间有一条鸿沟，象征问题尚未解决，我们的任务就是将未知量与已知量联系起来。

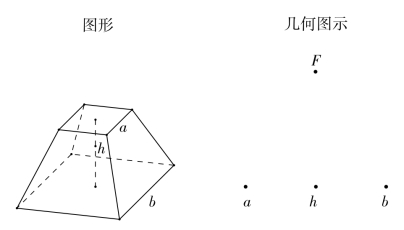
图3－7

第二，拟订计划。

问题3：怎样才能求得F？

由于我们已经知道棱柱、棱锥的体积公式，而校台的几何结构（棱台的定义）告诉我们，棱台是“用一个平行于底面的平面去截梭锥”，从一个大棱锥中截去一个小棱锥所生成的。如果知道了相应两个棱锥的体积B和A，我们就能求出棱台的体积

F＝B－A。①

我们在图示上引进两个新的点A和B，用斜线把它们与F联结起来，以此表示三个量之间的联系（图3－8）。这就把求F转化为求A和B。

图3－8

问题4：怎样才能求得A和B？

依据棱锥的体积公式，底面积可由已知条件直接求得，关键是如何求出两个棱锥的高。并且，一旦求出小棱锥的高x，大棱锥的高也就求出，为x＋h。

我们在图示上引进一个新的点x，用斜线把A与x，a联结起来，表示A能由x，a得出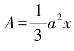，；类似地，用斜线把B与b，h，x联结起来，表示B可由b，h，x得出，B＝（图3－9），这就把求A，B转化为求x。

图3－9

问题5：怎样才能求得x？

为了使未知数x与已知数a，b，h联系起来，建立起一个等量关系，我们回忆处理立体几何问题的基本经验，进行“平面化”的思考。用一个通过高线以及底面一边上中点（图3－10中，点Q）的平面去截两个棱锥，在这个截面上有两个相似三角形能把a，b，h，x联系起来（转化为平面几何问题），由△VPM∽△VQN，得

这就将一个几何问题最终转化为代数方程的求解，解方程②便可由a，b，h表示x，在图示中便可用斜线将x与a，b，h联结起来。至此，我们已在F与已知数a，b，h之间建立起了一个不中断的联络网，解题思路全部贯通。

图3－10

第三，实行计划。

作辅助线（过程略）如图3－10所示，由相似三角形的性质，得

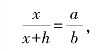(www.xing528.com)

解得

进而得两锥体的体积为

得棱台体积为

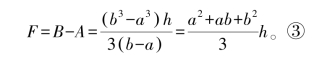
第四，回顾。

（1）正面检验每一步，推理是有效的，演算是准确的。再作特殊性检验，令a→0，由③式可得正四棱锥的体积公式；令a→b，由③式可得正四棱柱的体积公式。这既反映了新知识与原有知识的相容性，又显示出棱台体积公式的一般性；既沟通了三类几何体极限状态间的知识联系，又可增进三个体积公式之间联系的记忆。

（2）回顾这个解题过程可以看到，解题首先要弄清题意，从中捕捉有用的信息（如图3－2所示，有棱台，a，b，h，F共5条信息），同时又要及时提取记忆网络中的有关信息（如回想：棱台的定义、棱锥的体积公式、相似三角形的性质定理、反映几何结构的运算、调动求解立体几何问题的经验积累等6条信息），并将两组信息资源作合乎逻辑的有效组合。这当中，起调控作用的关键是如何构思出一个成功的计划（包括解题策略）。由这一案例，每一个解题者可以根据自己的知识经验各自进一步领悟关于如何制订计划的普遍建议或模式。

（3）在解题方法上，这个案例是分析法的一次成功应用。为了求F，我们只需求A，B（由棱台体积到棱锥体积的转化——由未知到已知，化归）；为了求A，B，我们只需求x（由体积计算到线段计算的转化——由复杂到简单，降维）；为了求x，我们只需建立关于x的方程（由几何到代数的转化——数形结合）；最后，解方程求x，解题的思路就畅通了。当初各自孤立而空旷的画面上（图3－6），形成了一个联结未知与已知间的不中断网络（图3－10）。书写只不过是循相反次序将网络图作一叙述。这个过程显示了分析与综合的关系，“分析自然先行，综合后继；分析是创造，综合是执行；析是制订一个计划，综合是执行这个计划”。

（4）在思维策略上，这个案例是“三层次解决”的一次成功应用。首先是一般性解决（策略水平上的解决），把F转化为A，B的求解（F＝B－A），就明确了解题的总体方向；其次是功能性解决（方法水平上的解决），发挥组合与分解、相似形、解方程等方法的解题功能；方梓等方法的解题功能；最后是特殊性解决（技能水平上的解决），比如按照棱台的几何结构作图、添加辅助线找出相似三角形、求出方程的解、具体演算体积公式等，是对推理步骤和运算细节作实际完成。

（5）在心理机制上，这个案例呈现出“激活——扩散”数学证明思维的基本过程。首先在正四棱台（条件）求体积（结论）的启发下，激活了记忆网络中棱台的几何结构和棱锥的体积公式。然后，沿着体积计算的接线向外扩散，一次激活截面知识、相似三角形知识、解方程知识（参见图3－6～图3－10），直到条件与结论之间的完全沟通。

（6）在立体几何学科方法上，这是“组合与分解”的一次成功应用。首先把棱台补充（组合）为棱锥，然后再把棱锥截成（分解）棱台并作出截面，这种做法在求棱锥体积时曾经用过（先组合成一个棱柱、再分解为三个棱锥），它又一次向我们展示“能割善补”是解决立体几何问题的一个诀窍，而“平面化”的思考则是沟通立体几何与平面几何的一座重要桥梁。这些都可以用于求解其他立体几何问题，并且作为一般化的思想（化归、降维）还可以用于其他学科。

（7）“你能否用别的方法导出这个结果？”在信念上，我们应该永远而坚定地作出肯定的回答，操作上未实现只是能力问题或暂时现象。对于本例，按照化棱台为棱锥的同样想法，可以有下面的解法。

如图3－11所示，正四棱台ABCD－A1B1C1D1中，联结DA1，DB1，DC1，DB，将其分成三个四棱锥D－A1B1C1D1，D－AA1B1B，D－BB1C1C，其中

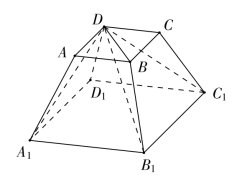
图3－11

图3－12

为了求VD－AA1B1B，可以联结AB1，将其分为两个三棱锥D－ABB1与D－AA1B1（图3－12），因

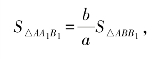
故

而

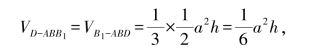
故

从而

（8）“你能不能把这一结果或方法用于其他问题？”能！至少我们可以由正四棱台的体积公式一般化为棱台的体积公式（方法也一样）。注意到

可得到一般棱台的体积公式为