小学数学化流程图运算生成

1.何谓“数学化”？

简而言之是数学地组织（在观察、认识和改造客观世界的过程中，运用数学的思想和方法来分析和研究客观世界的种种现象并对其加以整理和组织）现实世界的过程。

2.怎样“数学化”？

（1）横向数学化：即对客观世界的数学化。将现实中蕴含的数学知识抽象出来，形成数学符号、概念、图式、模型等。（从现实到符号）

图3－1　横向数学化流程图

【案例分析】

加法概念的形成：由“第一天有2只羊，第二天增加了2只，第三天又增加了2只，一共有几只羊？”这个问题抽象出“2＋2＋2＝？”

（2）纵向数学化：即对数学本身的数学化。在数学内部进行模式的生成、重塑、重组，形成不同层次的公理体系和形式体系。（从符号到概念）

图3－2　纵向数学化流程图

【案例分析】

乘法运算的生成：由“2＋2＋2＝？”这个问题可以转化为“2×3＝？”(www.xing528.com)

3.“数学化”的案例。

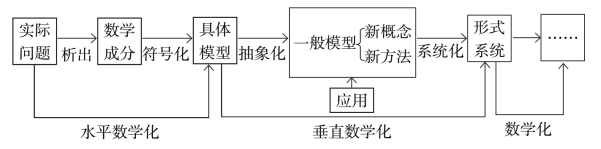
图3－3　数学化基本结构图

“七桥问题”与“图论”：18世纪初，普鲁斯首府格尼斯堡市内有一条河，河里有两个小岛，有七座桥把两个小岛和河岸连接起来。一个游人能否不重复、不遗漏地一次走完七座桥，最后回到出发点？

欧拉数学化的过程：

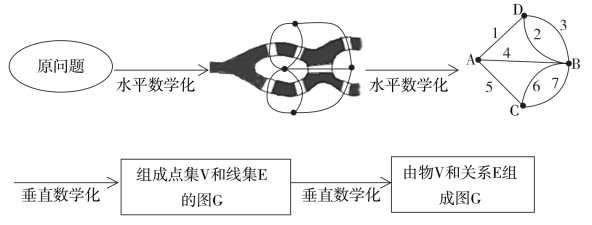
图3－4　“七桥问题”数学化过程

【项目设计】

试题（国家教师资格证考试·数学学科知识与教学能力（高级中学）模拟试题）：写出“鸡兔同笼”问题的数学化过程。

“鸡兔同笼”问题：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

解析：

图3－5　“鸡兔同笼”问题数学化过程