理性保险选择：重疾险保单分析，高保额方案推荐

整体而论，以上分析主要是基于定性分析，而具体的定量分析并未展开。对此，我们在本小节中围绕着理性保险决策的定量分析来展开，以帮助消费者获得保险配置的最大实效。就配置策略而言，我们整体上遵从“先保障基础，后个性化补齐”的配置思路。最终，我们需要达到“保额充足、保障全面、保费合理”的配置效果，以实现实效最大化。

1.配齐基础保障

我国保险业目前处于较为初级的阶段，保险渗透率相当低。以重疾险为例，截至2018年底，重疾险人口覆盖率^[24]仅为12.0%。其中，重疾险的有效存量保单的件均保额仅为107509元，31.5%的重疾险保单件均保额低于4万元，件均保额超过50万元的保单仅占到1.6%。^[25]

关于保险配置的金额，对于绝大多数消费者而言，应该先将保障类险种（寿险、重疾险、意外险、医疗险）的基础保额配置齐全。在此，我们将基础保额暂且定为50万（或100万）。对于该基础保额，每个人一律配齐。

50万元能解决什么问题呢？事实上，50万元仅仅只能为发生风险事故的家庭提供一个缓冲而已。身故风险、意外伤残风险等带来的收入能力损失通常远远超过这一水平。而对于重疾风险，医疗险往往仅能解决首期的医疗费用，之后往往存在续保难题，而后期的康复费用、护理费用等费用支出往往也是不菲的。例如甲状腺癌，虽然并不严重且医疗花费也较少，但是后期因为切除甲状腺而带来的额外护理费用和长期治疗费用等费用却并不少。另外，从第三章的重疾数据分析可知，一生中罹患28重度疾病的概率为男性65.6%，女性61.0%。这就意味着，人们一生中罹患重疾属于大概率事件，无论是否购买重疾险，绝大多数人都需要为此准备一笔资金用来应对重疾。其不确定性在于，什么时候会用到这笔资金。

同样，寿险50万元保额也就只属于基础保险金额。身故风险所导致的收入损失极大，尤其是对于年轻人而言。一般而言，人们在退休前身故所伴随的未来收入损失远超50万元，因此有必要配置高额的定期寿险。

就保险金额来看，讨论基础保额基于两点：第一，基础保额所覆盖的是人生中必然或者大概率所面临的支出；第二，现如今国内保险渗透率太低，相当数量的人群连基础保额都未能获得，而这也正是讨论基础保额的原因所在。

正是因为基础保额对应着人生中的必然或者大概率所面临的支出，因此才需要人人配齐。在为家庭成员购买保险时，父母通常优先为子女购买保险，而并非为自己优先购买。人们往往认为这种做法不合理，因为大人是家里的经济支柱，大人比小孩更应该优先配置保险。然而，笔者并不完全认同，因为给小孩配置基础保额的所需保费较低，获得基础保障仅只需要为数较少的保费，并不足以上升到优先为谁配置保险的高度。当然，如果真需要上升到优先给谁配置的话，笔者也同样赞成优先给大人配置保险，一是从紧迫性来看，大人的风险概率更高，紧迫性更高；二是从风险损失来看，大人的风险损失更高，配置所获得的效用更大；三是从保费涨幅来看，大人的保费基数更大，延迟投保所造成的保费涨幅更大，优先配置有利于节约资金。

事实上，与其说父母优先为子女配置保险不科学，倒不如说是父母只是想把最好的都先给子女。而之所以出现上述情形，主要是人们对保险依然不够了解而已。在配齐基本保障方面，优先为谁配置本身并不是问题，关键是为每个人都进行配置以化解整体的风险。

2.个人定制

配齐基础保障仅仅只是帮助诸多消费者快速制定保险需求的一个参考而已，更多的只是我国保险业渗透率较低的一个特殊时期的参考意见。事实上，基础保障并不能真正解决人们所面临的风险问题。根据个体实效理论，人们购买保险应该切实立足于解决所面临的具体问题，而每个人或者家庭所需要解决的问题又不尽相同。

每个家庭或个人的情况各不相同，因此所需的险种和保额也各不一样。对此，建立一套合理的、动态的配置标准，或者说是保险配置最大实效化的方法就很有必要。在此，我们需要对保障类型重新做定义，以方便我们进行合理计算和配置。

家庭财务缺口：指的是被保人本人发生收入终止的情况下（身故或者失能），为了保证家庭正常运转所需要的财务费用总额与家庭当前已备资金之间的差额。换言之，家庭财务缺口是当前储蓄情况不足以完全覆盖的必要费用的缺口金额。

家庭财务缺口的来源有很多，父母的孝养金、子女的教育/婚嫁费用、剩余的房贷/车贷，或者是其他必要的储蓄准备。通常，人们最容易想到的财务缺口是房贷，因为房贷金额较大，一旦家庭收入终止，房贷压力往往会给家庭造成巨大负担。

医疗保障：住院医疗费用分布呈现尖峰厚尾的状态（参见第七章），单次住院的高额花费整体上所占比例较小。这也就意味着，人们只需要少量的保险费用就可以获得很高的医疗保险保障。目前保险市场有着大量的“百万医疗”险种，因此，我们可以直接默认住院医疗保险保额为100万。在前面章节，我们也根据医疗费用的分布情况设计了“小额医疗+百万医疗”的方案，并针对医疗险的续保难题提出了解决方案，即分别配置不同公司的产品。当然，无论我们如何优化配置方法，目前依然难以解决医疗保险所面临的续保困境。

重疾保障：重疾保障用以解决由重疾风险导致的损失，该损失包括医疗险所不能覆盖的部分医疗费用、后期康复费用、理疗费用等。为了方便，我们可以将该笔费用保守地按照50万来计算。除此以外，重疾风险还可能导致短期内收入中止甚至永久性地收入终止。对此，我们在原来的基础上加上5年的年收入作为重疾保障的保守额度，即重疾保额=50万+5倍年收入。

身故保障：身故保障是用来解决身故风险所导致的损失，以身故作为赔付条件，不对身故原因（意外、疾病）进行单独区分。身故风险必然导致收入终止，因此，身故保障的目的在于解决个人当前所面临的家庭财务缺口。在此，规定家庭财务缺口大小即为身故保障金额。

未来收入保障：无论是身故或是残疾，都将对未来收入造成重大影响，譬如，家庭财务缺口产生的根源在于收入终止。虽然我们通过身故保障解决了家庭财务缺口的问题，然而，家庭财务缺口通常远小于未来收入。因此，对未来收入进行锁定也十分必要，只是优先级相对靠后而已。未来收入保障对于解决失能风险是极为有利的。医疗保障用以解决意外和疾病风险导致的住院医疗费用损失，身故保障用以解决身故风险的损失，重疾保障用以解决重疾风险的损失，但是，以上保障均无法解决“人活着，却因失能无收入”的风险损失。在此，我们规定：未来收入保障金额=未来总收入-身故保障金额。

失能风险对应有护理保险和失能保险，在此不再对其讨论，消费者可根据自身需求配置即可。然而，护理保险和失能保险并不能完全解决人们因为失能导致的收入损失，而意外伤残保险则对应着分别有意外伤残赔付责任和意外身故赔付责任。另外，未来收入保障金额往往较大，且意外伤残保险的费率较为便宜。因此，我们采用意外伤残保险来应对解决未来收入损失风险，以此作为未来收入保障的最低配置标准。

养老保障：养老保障的配置相对而言较为容易，并且其取决于人们对养老品质的要求，要求越高，所需的养老保障金额越大。另外，相比而言，养老保障存在多种可替代方式，即可选养老渠道较多，如房产养老、子女养老等。因此，在此不再对养老保障做过多展开。虽然目前保险市场缺乏纯养老年金保险，但可以通过一些变种养老年金保险进行替代。

医疗保障可以采用费率便宜的“百万医疗”进行解决，而养老保障的弹性较大。因此，我们接下来主要将重疾保障、身故保障、未来收入保障转换为对应的保险品种，并确定其保额。

重疾保障对应的保险品种为纯重疾险；身故保障对应的保险品种为寿险；未来收入保障对应的保险品种为意外险。它们分别对应的保额关系如下：

纯重疾险保额=重疾保障=50万+5倍年收入；

寿险保额=家庭财务缺口；

意外险保额=未来总收入-财务缺口=未来总收入-寿险保额。

关于以上财务缺口和保障金额，我们可以用表13-1的家庭信息调查表来进行相关计算，最终得到表13-2所示的费用汇总情况和表13-3所示的保障汇总情况。为了方便使用，笔者将以下表格做成相关网页链接，在填写表格后自动生成相应报告，读者可以直接在微信公众号“挖井人”中获取。

表13-1　家庭信息调查表

续表

①　平均余命，指人们从当前年龄始，至预期死亡时间止的期间，等于预期人均寿命减去当前年龄。

表13-2　费用汇总

表13-3　保障汇总

续表

对于大部分人而言，认真填完表格后都可能出现财务缺口。而这也正是大部分中年人焦虑且不敢轻易辞职的根源所在。同时，中年人面对着巨大的财务缺口，不仅不敢轻易辞职，更是不敢生病，脆弱的抗风险能力使得人们如履薄冰，战战兢兢。

面对诸多的不可抗力因素，当人们试图用保险来转嫁风险，提高抗风险能力时，却又觉得保费高昂。对此，合理的险种搭配也就显得十分有必要，因为我们还没到“不差钱”的程度。在前面，我们只是将对保障进行细化，然而并没有对保障的期限进行限制。也就是说，人们可以通过调整保险的保障期限，从而在确保有充足保障的情况下不造成过大的缴费压力。譬如，对于房贷，可以用定期寿险或者定期重疾来进行保障，因为保障期限相对较短，缴费压力较小。(www.xing528.com)

由于家庭情况会随着时间动态变化，人们可以每年定期做一次检视，补充、剔除，或更换之前的部分险种。譬如，随着收入的提高，可以考虑将原来险种的保障期限调长或者更换为保障更为全面的险种。

当然，部分人群由于有较多的财富积累，并不存在财务缺口，这表明其自身的抗风险能力相对较强。对于这部分人群，将财务缺口设置为零，把保障重心放在后续的几个配置目标上，并且可以调整险种和适当增加保费。

需要注意的是，以上的保险配置只是在尽可能减轻缴费压力的情况所做出的险种搭配设计。譬如，在解决家庭财务缺口问题时，选用的是寿险而非重疾险，原因在于重疾险相对而言费率更高，但重疾风险同样也会导致家庭财务缺口；在解决未来收入损失时，选用的险种是意外险，但疾病风险同样也可能导致收入终止，只是相对于家庭财务缺口而言，其带来的危险程度相对较低而已。因此，人们在可分配收入相对充足的情况下，可以尽可能将这些险种的保障范围进行“升级”，替换对应的险种。譬如，可以根据自身经济情况用寿险或重疾险来解决部分未来收入损失风险，同样也可以将部分寿险更换为重疾险等。

另外，我们采用意外险来解决未来收入损失风险，其依据是实效理论的第三条要素，对于“小概率风险”，可以衡量投保的机会成本。因为意外伤残保险所保障的是未来收入损失，在已经解决了家庭财务缺口的情况下，即使没有该部分保障，家庭运转也不至于完全沦陷。对此，消费者既可以通过购买保险来获得保障，也可以不购买，但是建议至少通过购买意外险来获得保障。对于经济条件宽裕的家庭，也可以考虑更换为寿险或者重疾险，具体视个人风险喜好程度而定。

3.保费预算

在保险配置中，保费合理同样是一个重要的考虑因素，毕竟保险配置不宜导致过大的财务负担。但是具体多少比较适合呢？

对于保障类保险，目前市场上比较流行的是“双十原则”，即用10%的年收入，配置10倍年收入的保额。“双十原则”有其实用性，但缺乏合理依据，其忽视了人们可支配收入的影响和保险配置的目的。我们姑且将“双十原则”认为是人们的一种经验准则。

根据实效理论，所有保险产品所赔付的期望值均为净保费（或其未来价值），产品之间并无本质区别。因此，对于多少保费合适的问题，不妨可以看成是人们愿意为想要的保险保障支付多少成本。

保单持有人与保险公司构成债务债权关系，保单持有人所获得的是对债务的索取权。从这个角度来说，保单持有人的债权多少往往是与保费多少呈正相关的。因此，必要的预算是保险配置的基石。但同样重要的是，合理的预算更是消费者理智的选择，避免不必要的花费才能实现自身利益的最大化。因此，对于消费者而言，选择性价比高的保险产品是同时获得优质保障和控制保费的有效措施，而这也正是本书所希望达到的目的。消费者应该为必要的保障留够保费预算，同时也要避免为不必要的保障和“溢价”买单。

保险除了保障功能外，还有“储蓄”的功能。对于储蓄功能，从某种意义上来说，其跟是否购买保险本身并没有关系，毕竟这些资金都是需要人们自行准备的。由此可见，“双十原则”作为一种经验准则，有着极大的局限性。

综上所述，关于保费预算，我们可以建立以下几点认知：①如果统一选择短期保险产品，人们只需要极少的年交保费即可构建足额的保险保障；②通过选择不同保险期限的产品进行组合，可以将保费控制在自己可接受的范围之内；③获得相同时长的保障，长期保险（均衡费率）的总保费比短期保险（自然费率）的总保费更少；④随着保险期限的延长，所承保风险通常变成大概率风险甚至必然风险，此时保险具有极强的“储蓄”性质，如终身型重疾险和终身寿险；⑤保费的多少本质上是保单持有人对保险债权的索取大小。

简而言之，人们可以通过较低的保费获得较高的保险保障，但是不能以此获得长期的高额保障；保费的多少并不构成保险配置的关键，而只是保险债权索取权的大小而已；保费预算的关键在于避免为非必要的溢价和保障买单，而非限制具体的金额或者资金占比。如果人们更加注重保险的保障属性，则所需的保费占收入比可以远低于10%；如果人们更加注重保险的储蓄属性，则所需的保费占收入比则可以远超过10%，其具体情况视个人而定。这就好比是租房和买房，两者均能获得房屋的居住权，但是买房才能获得房屋的所有权及产权，但是买房的缴费压力远远大于租房。

【注释】

[1]虽然保险定价中存在预定利率，但预定利率本身起到的是将未来保费进行折现的作用，并不构成其他影响。

[2]Daniel Bernoulli.Exposition of a New Theory on the Measurement of Risk［J］.Econometrica，1954，22（01）：23-36.

[3]一个人的效用应是财富的函数，这个函数称为效用函数。从理论上来讲，可以通过一系列心理测试来得到每个人的效用函数。不同的决策者应有不同的效用函数。伯努利认为，一定的财富状态或财富值对应一定的效用水平，一定的效用水平代表着一定的快乐程度。如果A和B具有相同的伯努利效用函数，则只要其财富水平相同，A和B的快乐程度就应该相等。

[4]林登.进化的大脑：赋予我们爱情、记忆和美梦［M］.沈颖，等，译.上海科学技术出版社，2009.

[5]乔纳森·海特.象与骑象人：幸福的假设［M］.李静瑶，译.杭州：浙江人民出版社，2012.

[6]Hacking Ian.Strange Expectations［J］.Philosophy of Science，1980（47）.

[7]图13-2中的数据获取步骤为：第一步，首先随机生成1亿局抛掷游戏的模拟数据，获得1亿组抛掷次数和奖金值的数据样本池；第二步，从所获得的1亿组数据样本池中有放回（即样本池数据不减少）地、随机地抽取N组（N以1000为间隔，上限设为1000万）数据来构成抛掷N局的数据集，并求出对应的奖金期望值（该步骤重复9次）；第三步，对新获得的抛掷N局的9个数据求中位数，生成最终的抛掷N局的期望值（即图13-2中对应的散点）；第四步，对最终获得的抛掷N局的中位数数据进行数据拟合，得到拟合曲线。需要说明的是：首先，模拟中的实验局数在理论上可以无限高，但受制于计算机内存容量和运算效率等因素，须酌情考虑具体的局数设置；其次，第二步中的抽取局数上限设为1000万，是因为需要预留足够数量的样本，消除数据样本可能产生的不利影响（即随着N不断增大，所获得的奖金期望值不断趋向1亿局对应的奖金期望值）；再者，对每个抽取局数随机抽取9次数据并以中位数而非平均值作为最终数据结果，是为了进一步减少随机误差造成的不利影响；最后，选用从已有的1亿局数据中随机抽取数据来生成其他对应局数的数据，而非直接重新模拟生成数据，是因为需要生成的数据量和对应的运算量极大，采用随机抽取数据来替代重新生成数据的方式对应的效率最高。对此，读者可下载代码后结合自身的电脑性能重新设置模拟参数来进行模拟。

[8]崔书英，马谦杰.圣彼得堡悖论的消解与决策学意义反思［J］.西南示范大学学报（人文社会科学版），2004（5）.

[9]选择2n-1局是为了方便局数分配，因为2n-1=1+2+22+23…+2n-1。

[10]此处默认n取值较大，因为n取值较小时式中的近似取值偏差极大。

[11]log2（10·N）=log2N+log210≈log2N+3.32。

[12]对于几何分布G（p），其期望值为，方差为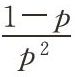，其中p为事件单次发生的概率。在该抛掷实验中，p=0.5。

[13]邓宁格：《工会与罢工》第36页。见《资本论》第一卷，第839页，人民出版社1958年版。现在比较流行另一个版本是：只要有10%的利润，资本就会蠢蠢欲动；有20%的利润，资本就会跃跃欲试；有50%的利润，资本就会积极冒险；有100%的利润，资本就敢于触犯法律；有300%的利润，资本就敢于冒杀头的风险践踏人间的一切法律。

[14]中文版可见：Daniel Kahneman，Amos Tversky，胡宗伟.前景理论：风险决策分析［J］.经济资料译丛.2008（01）.

[15]在原文中，这两个问题分别位列问题11和问题12。为了方便叙述，在此对其原文稍微作了调整。

[16]郭振华，朱少杰.小概率风险的判断与保险决策——经验决策理论的视角［C］.//全面深化改革：战略思考与路径选择——北大赛瑟（CCISSR）论坛文集·2014.2014.

[17]郭振华，朱少杰.小概率风险的判断与保险决策——经验决策理论的视角［C］.//全面深化改革：战略思考与路径选择——北大赛瑟（CCISSR）论坛文集·2014.2014.

[18]郭振华，朱少杰.小概率风险的判断与保险决策——经验决策理论的视角［C］.//全面深化改革：战略思考与路径选择——北大赛瑟（CCISSR）论坛文集·2014.2014.

[19]存在保险定价附加保费，因此被保人应当自留部分风险进行“不足额投保”。

[20]路遥.平凡的世界［M］.北京：北京十月文艺出版社，2013.

[21]对于健康保险，通常补偿型保险都会设置上限保额，这使得补偿型的健康保险（如医疗险）属于劣质商品。但是财产险则较为特殊，财产保险的保额取决于财产的价值，财产越多，导致风险损失越大，因此需求是增加的，此时财产保险不能完全列入劣质商品，可参见第十六章。但是，对于财产细分类，其本身都是有价值上限的，比如汽车、房产等，其对应的车损险、房屋火灾保险等在一定程度上都可以视为劣质商品。

[22]＞表示前者优先级高于后者，≥表示前者优先级不低于后者。

[23]根据《人身保险公司保险条款和保险费率管理办法（2015年修订）》，仅包含由意外伤害导致的医疗保险责任的保险应当确定为医疗保险。意外伤害医疗保险应当划归为医疗保险，但实务中的意外险通常包含意外伤害医疗保险责任。

[24]人口覆盖率指拥有有效重疾险保单的被保险人数与中国大陆人口数比值。

[25]中国精算师协会经验分析办公室.中国人身保险业重大疾病经验发生率表（2020）编制报告［M］.北京：人民日报出版社，2020.