理性保险选择：财富等概率随机分配

在此，我们设计相应的简化模型，假设所有参与者能够在每次分配中随机地等概率地获得财富。而这类似于知乎上的一个问题：“房间内有100人，每人有100元，每分钟随机给另一个人1元，最后这个房间内的财富分布怎样？”

结合该问题，我们设定100位25岁玩家均持有100元初始资金，然后每天进行一次游戏并把1元钱随机分给另一个人，一直持续到65岁退休。在这个简化模型中，每天随机给另一人1元可理解为基本消费，而其他任意某成员都可能随机获得这1元。直到最终结束，一共进行了14600（365×40=14600）次分配，为了方便，我们将分配次数定为15000次。在模拟结束后，各玩家的最终财富情况如图5-1所示。

图5-1　等概率分配中各玩家的最终财富情况

可以看到，经过15000次分配后，财富分布出现了分化，有人最后破产并且背负了债务，有人集中了大量的财富。从分布状态来看，最终的财富分布近似于“幂律分布”。当然，对于很多读者来说，幂律分布是一个很陌生的概念。相比而言，人们更为熟悉幂律分布的另一种表现形式——二八定律。19世纪，意大利经济学家帕累托（Pareto）研究个人收入的统计分布时发现，少数人的收入要远多于大多数人的收入，提出了著名的“80/20法则”，又称“二八定律”，即20%的人口占据了80%的社会财富。(www.xing528.com)

当然，我们只是看到模拟结束的最终情况，并不足以说明这是否只是中间的一个偶然出现的结果。对此，我们可以把中间每一次分配导致的贫富分化状态表示出来，并且重复多次模拟。我们用标准差来表示整个群体的贫富分化状态，标准差越大，表明贫富分化越严重。如图5-2所示为5次模拟中玩家之间财富两极分化过程。

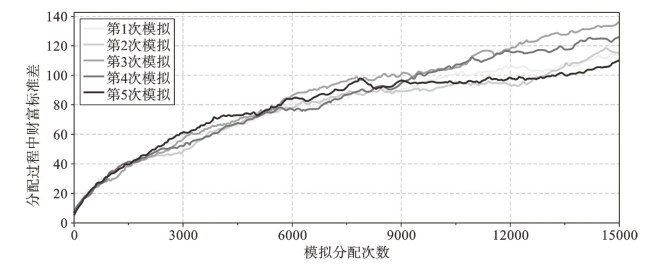
图5-2　等概率分配中财富两极分化过程

可以看到，多次模拟的结果：贫富分化的整体趋势在不断扩大。即便所有人的起点相同，每次获得财富的概率相同且随机，财富的两极分化也成为必然。当然，现实世界比这更加复杂，每个人的起始条件并不完全相同，富人与穷人同时参与。对此，我们不用再去直接重复模拟一遍，因为我们只需要随机地设定部分参与者为富人即可，而其他过程均相同。想象一下，如果富人的起始财富足够多，即使富人中有最败家的参与者，他最终或许依然处于富裕阶层。更何况，并不是所有高起点的参与者都是败家的。

在现实生活中，人们获得财富的概率并不见得完全相同，毕竟每个人的自身先天禀赋、后天努力和社会环境等因素存在差异，因此，我们共同来模拟人类财富不等概率随机分配。