儿童数学问题解决策略性知识的发展方法

达尔文曾经说过，最有价值的知识是关于方法策略的知识。儿童在数学问题解决的过程中发展策略性知识是十分重要的。由于儿童各个年龄阶段认知水平不同，因此，各个年龄阶段的儿童数学问题解决策略的发展也是有所不同的。

研究表明，第一学段（1～3年级）的儿童在数学问题解决过程中较多的是采用尝试、作图、实际操作、概括规律、列举信息等策略。而第二学段（4～6年级）的儿童，除了这些策略外，已经开始发展到较多的运用从简单情况入手、从相反方向去思考等策略了。

（一）尝试的策略

尝试策略就是多种方法的“试误”过程。不同的学生有着不同的数学水平，因此，要允许学生以不同的方式去学学习数学。教师所要做的，就是要充分尊重每个学生的个性差异，让学生采用尝试的策略去解决问题。

例如，“每条船最多可坐8人，50名同学需租几条船？”常见的做法是引导学生计算一下，50÷8=6（条）…2（人），故得知需租7条船。但这样的学习组织缺乏对问题多种解决策略的尝试和探索。因此，可以放手让学生自己去尝试探索：

（1）8×6=48（人），6条船可坐48人，多2个人，需租7条船。

（2）8个8个地加，共加6次余2人，需租7条船。

（3）从50里依次去掉8人，去6次后还有2人，需租7条船。

（4）如果每条船坐10人，50人租5条船，每条船多了2人，5条船就多算了10人，需再加1条船，余下的2人再租一条，一共租7条船。

（5）6×8=48（人），8×8=64（人），6条船只能安排48人，不够，而8条船太多了，所以7×8=56（人），比较合适的是租7条船。

当然，还可以借助学具操作，用小棒代表船，用圆片代表人摆一摆，从而获得结果。

（二）作图的策略

儿童因年龄的局限，对符号运算性质的推理可能会感到比较困难，运用作图辅助的策略，让他们在纸上涂涂画画可以拓展思路，帮助他们找到问题解决的关键。

例如：学校外有一条长50米的大道，在大道一旁栽上树，每隔5米栽一棵，路的两头各栽一棵，共需要树苗多少棵？如果大道的一头栽一棵，另一头不栽或两头都不栽树，又各需多少棵树苗？

分析：大道长50米，每隔5米分一段，可以分成10段。从图上明显可以看出：

（1）

栽树的棵数比分的段数多1，即栽树的棵数为：50÷5+1=11（棵）

栽树的棵数正好是分段的段数：50÷5=10（棵）

栽树的棵数比分的段数少1：50÷5-1=9（棵）

运用图形把抽象问题具体化、直观化，从而能帮助学生迅速地搜寻到解题的途径。因而，对学生进行画图策略的指导显得尤为重要。

（三）动手做的策略

这是一种通过探索性动手操作而获得问题解决的策略。需要注意的是，在学生动手操作之前，教师不要给太多的暗示，要把实际操作策略的选择权留给学生，让学生在自主探索中实现操作策略的多样化。(www.xing528.com)

例如，探究“梯形的面积计算方法”这一问题，教师先给出一个梯形的图例（当然也可以让学生自己构造一个梯形），如图14-5所示。

于是，学生可以通过自己的探究性的操作活动，将这个问题转化为一个已知的问题进行推导性研究：或者将它拆为两个三角形；或者通过割、补将它转化为长方形；或者通过构造一个全等的梯形，再拼成一个平行四边形；等等。通过这种开放性的操作策略，不仅有可能获得问题解决，而且还能培养学生的创造性思维。

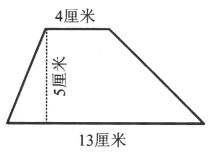
图14-5

（四）概括规律的策略

寻找规律是数学问题解决中最常用并且有效的方法。碰到较为复杂的问题可以先退到简单特殊的问题，通过观察，找出一般规律，然后用得出的一般规律去指导问题的解决。

如，“用3、4、5、6、7、8六个数字组成两个三位数，使这两个数的乘积最大，应怎样排列？”这道题若盲目拼凑，不但费时费力，也不易得出正确答案。可以引导学生先退回来研究与例题相类似、但较容易的特殊情形。如：“用1、2、3、4四个数字组成两个两位数，使两个数的乘积最大，应怎样排列？”然后再引导学生概括出解题规律：（1）较大的数应填在最高位；（2）较小的数与较大的数搭配写；（3）所组成的两个数的差应最小。由于学生通过分析数据发现和归纳了一些规律，再回过头来解答原题就较为容易了。

（五）列举信息的策略

有时，在解决问题过程中，将问题的条件信息用表格的形式列举出来，往往能对表征问题和寻找问题解决的方法起到事半功倍的效果。

例如，5元一支的圆珠笔和15元一支的钢笔共买了30支，一共花了350元，问两种笔各买了多少支？就可以指导学生运用画表列举信息的策略。

从表中可以看出，每增加一支15元的钢笔，所用的总钱数增加10元。这样，当总数从150元增加到350元，实际增加了200元，于是200÷10=20支，即15元的钢笔买了20支，5元的圆珠笔买了30-20=10支。这样，不仅让学生运用数学知识解决了生活问题，更重要的是运用制表策略很快解决了数学问题。

（六）从简单情况入手的策略

根据认识论原理，人们认识问题总是从简单到复杂，从个别到一般。所以，当我们面对一个复杂的问题感到束手无策时，不妨采用退的策略，从复杂的问题退到最原始、最简单的同构性问题，对它作一些探索，借以触发解题的灵感，找到解决原问题的突破口；或者通过对原问题进行分解转化，将其变化成若干个比较简单的问题，然后各个击破，分而治之，逐步达到解决原问题的目的。

例如：数一数下图共有（　　）条线段。

此题由于点数不确定，令学生感到无从下手。于是可以先出示几个简单的图形：

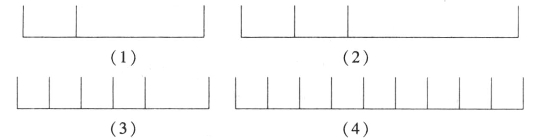
让学生分别去数一数它们各有多少条线段。然后引导学生观察点数与段数的关系，由此学生就可以把由探究简单问题得出的结论推广到一般情形：有n个点的线段共有n×（n-1）÷2条线段，复杂的问题由此简单化。

（七）从相反方向去思考的策略

在解决某一问题的过程中，当从正面进行思考而遇到困难时，如从相反的方向去思考，往往能起到意想不到的效果。从数学问题解决的方法看，它实际上就是一种“逆推法”，属于一种“分析”的思维路线。

例如，求1～100这100个自然数中不能被3整除的所有数的和。

此题若直接求“这100个自然数中不能被3整除的所有数的和”，难以找到线索，假如我们从相反的方向去思考，将问题改为求“这100个自然数中能被3整除的所有数的和”，问题就容易得到解决。

事实上，当一个数学问题呈现在面前时，其思维的触须是多端的。以上所述的几种问题解决的策略只是平时常用的导引途径，为了能够更有效地提高数学问题解决的能力，教师还要引导学生在数学问题解决的实践中注意不断思索探求、逐步积累解题经验，以掌握更多、更具体的解题方法和思维策略。