小学数学课程教学：问题解决心理模式

长期以来，许多的心理学家、数学教育家以及其他的学者，对问题解决的基本模式作了大量的研究。当然，这些学者的研究，往往建立在自己的哲学观与心理学基础之上，因此，归纳的问题解决过程模式也不尽相同。

（一）杜威（J.Dewey）模式

（1）情境。即创设一个真实的困难情境，使学习者产生一种认知的困惑感。

（2）问题。即在情境内部识别出问题所在，包括所寻找目标的一般标志和要达到的目的等。

（3）假设。即将问题情境中的问题与已有认知结构联系起来，以激活有关的知识背景以及先前的思维方法，提出解决问题的猜想、建议或暂时作出一些尝试性的解答。

（4）推理。即根据假设一步一步地展开他所设想的解决问题的方法。

（二）纽威尔与西蒙的信息加工模式

纽威尔（A.Newell）与西蒙（H.Simon）以信息处理系统说明问题解决的心理过程，如图14-2所示：

图14-2

从图14-2可见，感觉神经接受问题所产生的刺激，并将信息（包括问题的信息与解决问题的标准）传递给处理者。而所谓处理即为认识过程，它根据已有的学习或经验中所获得的解决问题的程式或策略对信息进行处理，若需要所记忆的有关原则，可以自动求助于记忆系统。在问题解决过程中，处理者从记忆系统中提取信息的过程，是往返不停的活动。若现存记忆不敷所需或因遗忘而无法提取时，处理者或者停止解决问题，或者重新进行学习，以便继续解决问题。这时，作用者将处理者提供的有效解答揭示出来，揭示方式有语言表达或动作表现。

（三）波利亚的解决问题四阶段模式

波利亚曾给出了一个简明的数学问题解决的四阶段模式，揭示了解决数学问题的心理活动历程。(www.xing528.com)

（1）理解问题。首先，必须弄清楚问题的求解目标是什么，并使其目标在脑海中留下深刻的印象。其次，弄清楚已知条件是什么，明确任务：如何在已知与未知之间架起桥梁。

（2）设计求解计划。先观察能否在已知条件与未知解答中直接架起桥梁。倘若不能，就得采用迂回的策略设计辅助问题，以求达到目标。通过辅助问题的解决在已知与未知之间建立联系，形成一条通道。

（3）实现求解计划。将探索到的解题方案进行逻辑整理，并且用语言将其表达出来。

（4）检验和回顾。检验所得结果是否符合实际，回顾解题过程中的关键，探索更好的方法。

（四）奥苏伯尔等的问题解决模式

美国心理学家奥苏伯尔与鲁滨逊（P.G.Robinson）于1969年提出了问题解决的模式，该模式不仅描述了问题解决的基本过程，而且着重说明了认知结构中各成分在解题过程中的作用，对我们研究小学数学问题解决的过程是颇有帮助的，见图14-3。

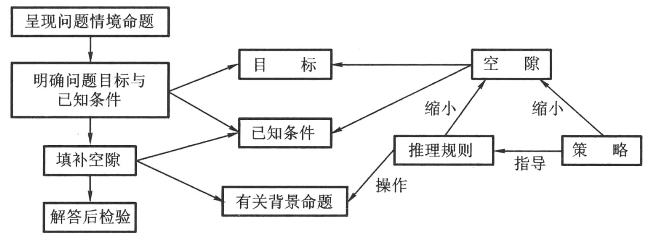
图14-3

（1）呈现问题情境命题。一般是对问题的全面描述。如果学习者具有相关的背景知识，就容易呈现问题的情境，并将其与原有的认知结构相联系，有利于理解题意。

（2）明确问题目标与已知条件。对复杂问题的目标与已知条件的全面了解往往需要进行反复的表征才能实现。

（3）填补空隙过程。在填补起始状态与目标状态的空隙过程中，至少涉及三个要素。一是有关的背景命题，这是指学习者能从原有认知结构中提取出所要解决问题的有关概念、事实和知识；二是推理规则，学习者能遵循逻辑原则作出合理的推理；三是学习策略，指选择、组合、改变或操作背景命题的一系列措施，以填补目标与条件之间的空隙，并尽量减少尝试错误的任意性，节约解决问题的时间。

（4）解答后检验。问题一旦解决，需作一定回顾，进行一定形式的检查，查明推理有无错误，思考过程是否简捷。