小学教学：儿童学习统计与概率的特征

在开始学习之前，大部分儿童在描述一个现象的时候，往往简单地通过对现象的直观认识来描述，他们往往还不会通过收集数据，并利用数据对这些现象进行更为精确的描述或预测。而儿童的统计与概率思想的形成，不仅有赖于他们对知识的学习，还有赖于遵循他们发展规律的教学组织。

（一）统计思想的形成

统计思想的本质是从局部观察到的资料的统计特征来推断整个系统的状态，或去判定某一论断能以多大的概率来保证其准确性，它是一种由局部推断整体的思想方法，是一种探知某个系统的规律性的科学。儿童在形成统计思想方法的过程中，主要会表现出如下一些特征：

图13-1

（1）儿童的统计思想是在操作活动中逐步形成的。例如，一个学龄前的儿童，面对由许多香蕉和苹果组成的一堆水果时（图13-1），在开始的时候，可能只会采用先数出香蕉的个数，再数出苹果个数的方法来比较哪种水果多。但是，当这些水果的数量足够多的时候，慢慢地，他可能就会想到将这些水果先分开来，然后再分别去数。随着经验的增长，他可能逐渐会想到将这些水果分类对应排列起来（图13-2），于是，对这个儿童来说，基本的统计思想就产生了。

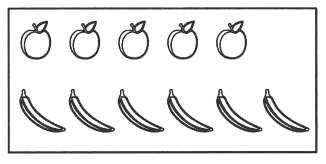
图13-2

（2）儿童对数据的分析与利用能力的发展是一个渐进的过程，对一个学龄前的儿童来说，数字往往只是表示单个物体量的一个符号，并不用来描述自己观察到的现象。因此，数字之间往往是不相关的。例如，他可能关注到，有一个小朋友一天里吃了1个水果，吃了5块巧克力糖。然而，在他眼里，这些只不过就是一些静止的和不关联的数字，他也只是获得了一些事实。可是，对于一个低年级的小学生来说，他可能已经能从这两个似乎不关联的数字中，推断出“这个小朋友可能偏爱巧克力糖而不太喜欢水果”这样的结论来。而对于一个更高年级的儿童来说，他可能已经会从中受到启示，然后通过某些调查获取数据的方式，去选择类似“在校园里究竟是卖水果好些，还是卖巧克力糖好些”这样的行为了。

（3）在儿童的经验中，往往是通过对一组单一数据的比较，来作出简单的且具有唯一性的判断。当他们在最初接触到一组复杂数据的时候，往往就会采用经验中的方法来作出判断或无法作出判断。例如，小明一分钟拍了20下皮球，小红一分钟拍了25下皮球。这样的数据说明了什么？对于这个问题，一个学龄前的儿童也能作出准确的回答。可是，许多低年级的学生，面对如下一组数据的时候（表13-1），可能就不容易作出判断：“有A、B、C三个班举行长跑比赛，每个班级选出10人，其结果如下。现在你将如何确定这三个班长跑比赛成绩的好坏？能不能排出这三个班长跑比赛的名次并说明理由？”(www.xing528.com)

表13-1

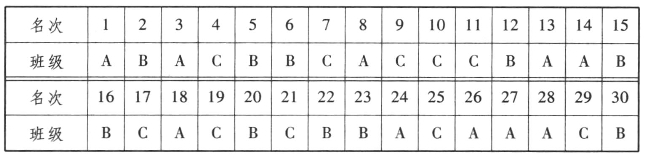
（4）统计往往需要选择样本，选择什么样的样本？选择多大的样本才合理？对一个低年级的儿童来说，这些可能都是比较困难的。因为在儿童的经验中，收集的样本常常都是可以穷尽的总数，例如问一下班级的所有同学，就知道班级里有29个同学不喜欢穿运动鞋，因为班级里有35位同学，所以就可以得到这样的结论：班级里大部分同学都不喜欢穿运动鞋。可是，是不是全校的同学中，也是大部分同学都不喜欢穿运动鞋呢？当学生调查另一个班级并发现只有9个人（班级人数也是35人）不喜欢穿运动鞋的时候，他们就会发现，这个结论并不适用于现在这个班级。当然，学生可能还是可以通过全部数据的调查来回答这个问题的，可是，当问及是整个城市中的同龄学生的时候呢？一个比较好的办法就是通过选择适当的对象和合适的范围进行调查，然后来推测。然而，这对一个儿童来说是比较困难的，因为他们的经验往往还不能有效地支持他们作出这种合适的选择。

（5）儿童主要是从“大、小”开始认识数的，因而，对低年级的儿童来说，他们往往对数据的“最大”或“最小”比较敏感，当他们对一组数据进行排序的时候，最关注的是“谁大”或“谁小”这样的数据特征，而还不能将这一组数据作为一个描述现象的整体来看待。到了中、高年级，儿童已经开始知道，面对一组数据，不仅需要关注单个数据的特征，还要关注整个数据组的特征。例如，通过调查A、B、C、D、E、F、G等七位同学在一年内上电影院看电影的情况后，得知分别为：7次、5次、7次、9次、2次、7次和11次。对一个低年级的儿童来说，他们所能描述的可能就是E同学每年上电影院的次数最少，而G同学每年上电影院的次数最多。而对于一个中、高年级的儿童来说，他们可能已经会关注到，数据主要集中在“7”的周围，而且，相对于一年的时间来说，同学们每年上电影院看电影的次数是不多的。因而，对于他们来说，认识“平均数”、“众数”等的意义就比较容易了。

（二）对事件发生的可能性的认识

虽然在现实世界中存在着大量的确定现象与不确定现象，但是，对于儿童来说，他们要真正认识事件发生的确定性以及事件发生的可能性大小等概念，还是有一个发展过程的，在这个过程中，儿童主要会表现出如下一些特点：

（1）对儿童来说，对事件可能与不可能发生的情况，在低年级的时候已经经常遇到了。但是，他们还不能对事件发生的可能性情况作出一些预测。例如，面对一个一年级的学生，你将10个红球放入一个布袋，然后问他，现在老师随便从里面摸出一个球来，你能猜出是什么颜色吗？他当然能作出准确的回答，当你再问他，有没有可能摸出一个黑球来，他当然也能作出准确回答。可是，当你将5个红球和5个黑球放入布袋，再问他相同问题的时候，他就可能无法对结果作出准确的表述了，因为在他看来，这个问题是无法回答的。

（2）儿童对可能性的认识，主要源于他们的生活经验，因而在作出判断的时候，他们所处的环境与所经历的生活起着相当大的作用。例如，对于股市涨跌的可能性判断，对儿童来说是缺乏经验的，但是对于自己能否在考试中取得好成绩，他们却能预测。又如，对生活在南方的儿童来说，对于“明天是否会下雪”这样的问题，其回答与生活在北方的儿童可能是不同的。

（3）儿童对事件发生的可能性大小以及等可能性的认识，需要通过大量的操作活动来建立。例如，只有当儿童自己反复抛掷一枚硬币，然后通过对记录的数据进行统计与观察，才有可能发现正面朝上与反面朝上的次数这两个数据逐渐接近，因而有可能体验到这两者发生的可能性是一样的。当然，这里还包含着一个基本的极限思想的问题，因为还需要学生懂得，只有当事件的频数（抛掷硬币的次数）趋向无限大时，正面朝上与反面朝上的机会是相等的。又如，问一个一年级的学生类似“当你一打开电视机，在5分钟内就会看到广告节目的可能性有多大”这样的问题时，他们往往只会凭借经验的模糊印象给出某些猜测。而对于高年级的学生来说，他们可能已经会想到，先去统计一小时内广告节目出现的频率，然后依据收集到的数据作出判断。