儿童几何思维水平发展过程揭秘

儿童的几何（空间）思维水平的发展有明显的阶段性，而这个水平的发展不仅依赖于儿童逐渐的心理成熟，更依赖于教师的教学组织。因为教师可以将某一级水平的学习降低到较低水平（如死记硬背）来组织，所以，了解儿童几何（空间）思维水平的发展对教师组织几何教学是非常有价值的。

（一）儿童空间思维水平发展的阶段性

按照范·西尔夫妇的研究，人的几何思维有一个水平发展的阶段性^[1]，而且这种阶段性还表现出以下特点：第一，水平的发展基本上是非连续性的，说明几何思维的水平存在着一个不确定的性质差异；第二，思维水平是有层次的，绕过高一层次的教学，可能获得记忆，但不能获得这一层次的理解；第三，前一水平所蕴含的性质会成为下一水平的明确理解；第四，不同的水平层次有自己独特的语言符号系统以及联结这些符号的关系系统，因此，不同水平的推理在理解上是不同的。

从小学生几何思维水平的发展看，大致有以下阶段：

1.水平0

水平0被认为属于前认知阶段。在这个阶段的儿童，能感觉几何形状，但由于其感觉活动的不足，往往只能注意到对象的形状直观特征的某一部分。例如，有的儿童可能会区分直线图形和曲线图形，但对于同类图形（如正方形和平行四边形）不能正确区分，因此，面对一个给定的图形，他们常常不能重构一个与之性质相同的图形。

对处于水平0的学生来说，他们的思维特征就是依赖对象的具体想像或自己的触觉刺激，建立在“形状相同”这样的等级之上。

2.水平1

水平1被认为属于直观化阶段。在这个阶段的儿童，往往按照外观来识别图形，或者说只能建立一些关于“形状”的抽象，而并不关心图形的几何性质或一类图形的本质特征。他们的思维以知觉为主，因为他们可能会区别一些图形，但并不依据这些图形的性质，而是依据这些图形的外观与形状。因此，当两个图形看起来相同时，他们就会认为这两个图形是相同的。所以，他们在对一群对象进行分类时，更多的注意这些对象“具有什么样的形状”，而不是这些对象具有什么样的性质特征。

例如，这个阶段的儿童可能会区分矩形和三角形，是因为“矩形像门，而三角形不像门”，但是，他们可能不能区分正方形和菱形，认为他们都是“方的，像手帕”，所以他们是“相等”的。又如，他们无法区分二维的和三维的图形，他们会认为“长方形”和“长方体”的形状是一样的。

3.水平2

水平2被认为属于描述/分析阶段。在这个阶段的儿童，能通过观察、测量、搭建或绘画等活动，经验地建立图形的性质，并用日常生活的经验用语将这些性质描述出来，从而能将这些性质与一类图形建立联系。这时，图形的视觉特征有可能被单独感知，并且有可能将其联系到某一个文字的标记上，通过对直观特征的反思，从而能通过图形的性质来识别图形并确定图形的特征，还能用构造图形的路径来思考二维图形。例如，这个阶段的学生看到各种形态的三角形，都能准确的识别，而不管这些三角形在形状上有多大的差异。

对于水平1和水平2，莱勒等人曾作过这样一个测试^[2]：向学生呈现如下一些图形，

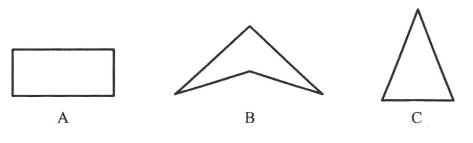
图12-3(www.xing528.com)

当问及哪两个图形最像时，处于水平1的学生会认为是B和C，并说明“B除了里面稍微有些弯以外，它和C看起来是相同的”，可见这样的学生注意到的是图形的直观方面；而有的学生会选择图形A和B，因为他们认为这两个图形都有四条边。显然，这样的思考已经开始倾向于忽视图形形状的直观因素，而凸现图形形状的性质因素。

但是，处于水平2的学生，他们对图形的分类依据一定的自己理解的性质，但不能在不同性质之间构建某种联系，所以往往还不能识别两类图形之间的关系。因此，让他们去理解正方形就是特殊的长方形，甚至去理解长方形就是特殊的平行四边形等，可能都是比较困难的。

4.水平3

水平3被认为属于抽象/关联阶段。在这个阶段的儿童，已经开始能形成抽象的定义，区分概念的必要条件和充分条件，开始注意到不同图形性质之间的关系，因而能分层次地将图形进行分类，并对这些类别进行非形式化的论证。例如，他们已经能够理解如图12-4所示的分类：

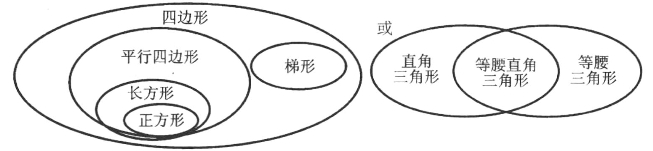
图12-4

同时，这个水平阶段的儿童，开始能依据图形的性质将图形进行组合或分解，他们能进行建立在操作性实验基础上的推论的空间思维活动。例如，他们能从长方形的性质特征出发，将一个平行四边形，通过自己的操作活动转化为一个长方形，从而推导出平行四边形的面积计算方法。又如，他们能理解任何一个四边形都可以被重组为两个三角形，就能从三角形的内角和是180°推导出四边形的内角和是360°。

此外，随着儿童空间透视能力的发展，他们开始能获得不同纬度图形的识别，能知道“长方形”与“长方体”之间的联系与区别，因为他们开始学会依据“面”这个元素来观察、认识三维图形的性质特征。

（二）儿童空间想像力的发展

加德纳认为^[3]，“空间智力的核心是准确感觉直观世界的能力，依靠人最初的感性认识形成变换和作出修正，即使在缺少相关物质刺激的情况下也能重建人们直观经验的方面”。所谓的空间想像能力，是指对客观事物的空间形式进行观察、分析、归纳和抽象的能力。一般地说，空间想像能力以良好的空间观念为基础，以形成空间概念为目的。

空间想像能力，其至少包含这样几个要素：第一，依据实物建立模型的能力；第二，依据模型还原实物的能力；第三，依据模型抽象出特征、大小和位置关系的能力；第四，能将模型或实物进行分解与组合的能力。

空间想像能力通常还具有两个明显的特征：首先，它具有较强的抽象性，即需要不断地从实物中抽象出模型；其二，它具有较强的想像性，这是空间想像能力的主要特征，而且几何纬度越高，对想像的要求也就越高。

低年级的儿童，对空间图形的想像还需要依附一定的直观物体的支持，例如，小学的几何学习基本上是从认识“二维图形”开始的，但儿童积累的却是大量“三维”的几何经验，因此，他们在对“二维”图形的空间思考的过程中，往往会依附相应的直观的物体（像长方形与长方体形状的物体相对应）。在教学组织中，教师又常常会引导学生去想：日常生活中有哪些物体是长方形的？强化了儿童在平面几何的思考中对直观物体的依赖性。有的学生甚至到了较高年级学习“圆的认识”的时候，在自己的空间思考时还会受到直观物体“圆球”的干扰。

儿童经过一段时间的学习后，到了3～4年级，他们已经开始有可能根据对象的性质特征，构造反映这个性质特征的模型，并以模型来思考。例如，这时的儿童在认识一些平面图形的性质特征时，已经开始不再将图形与相应的直观物体去对应，而只关注图形本身的性质特征。又如，他们在计算三角形面积时，懂得符号S△所表示的意义，可见，他们已经开始用符号构造关于三角形的模型，而并不去关注这是什么形状的三角形了。

到了再高些年级，儿童对图形的认识已经开始更多的依赖模型的构建了，例如，他们学习“长方体”、“圆柱体”等的性质特征时，观察对象主要是一些实物模型而并非直观物体，因而摆脱了对象的直观特征，思考的是对象的性质特征。