小学数学课程：培养数学概念能力

构建数学概念，需要学生具备一定的生活经验及数学认知结构，一定的数学思维能力和语言理解、记忆、表述能力。这些能力不是学生先天就有的，也无法从其他途径获得，只能在数学概念的构建过程中加强培养，才能逐步形成、逐步提高。因此，在数学概念教学中，要把培养学生构建概念的能力放在重要地位。

（一）重视表象的过渡

小学生的思维尚处在具体运算阶段（以直观思维为主）向形式运算阶段（以呈现思维为主）逐步发展的过程中，因此，形成数学概念往往有一个从直观到抽象的过渡，这个过渡就是“表象阶段”。表象就是对对象的一个整体的“映象”，而这个“映象”，包含着对象的本质的和非本质的所有属性，包含着对对象的外在认识，也包含着对对象的内在认识。是在直观感知基础上，并在语言（更多的是外部语言）支持下，通过对对象的分析与综合思考的产物，其基本特征就是还没有真正摆脱对具体对象的依赖，但它是儿童形成概念的一个重要的基础。

例如，在“9的认识”这样的“数”的概念学习中，教师或教材提供了大量的直观材料（各种有关“9”的具体形象）。在学生观察和体验过程中，要尽可能地引导学生去感知这些对象的某些基本特征，形成“9”就是表示有“9样东西”。这时，虽然认识本身还具有一个物质特征（如“东西”），但却已经开始能反映出这个对象的某些本质属性了。

在这个过渡的过程中，有三个方面需要引起注意。第一，在引导学生观察时，要让学生充分地明确自己的观察任务；第二，在学生在感知对象时，加强他们语言的运用；第三，在学生获得感知的基础上，要引导他们及时地归纳。

（二）加强数学交流

学会数学交流是培养数学素养的一个重要方面，而有效的数学交流依赖于准确的数学概念。因此，准确地运用数学概念是发展数学交流能力的一个条件，而充分的数学交流活动又能促进对数学概念的进一步发展。

1.表述和交流自己的发现

在概念学习的初始阶段，可以引导学生经常将自己观察、操作或比较后所获得的发现、体验等与同伴进行交流，学生可以通过对表述和交流所用语言的逐渐准确和精炼，帮助他们对概念的正确认识和掌握。

2.解释和说明自己的观点

数学交流能力的一个重要特征就是能将自己的观点或结论，用清晰的、简练的和准确的语言给予解释或说明。这个解释和说明的过程，不仅是一个理解数学概念的过程，还是一个运用数学概念的过程。

3.质疑和反驳他人的想法

数学交流不仅注重自己想法和观点的表述与证明，还应注重在倾听和接纳他人意见和想法的基础上，能经常主动地质疑和反驳。在这个过程中，学生一方面要能及时抓住他人在表述或说明中对人有启发的见解，并找到其本质性的问题所在，另一方面要学会用准确的数学概念来反驳他人的意见和想法，使他人能理解并接受。

（三）促进数学思维

数学思维能力是指保证数学思维活动能够顺利进行的个性心理特征。影响概念构建的数学思维能力主要有观察能力、分析比较能力和抽象概括能力。

1.发展观察能力

观察是人们有目的、有计划地感知和描述各种自然现象的一种思维方法。观察是获取感性认识的重要手段。观察能力是指通过数学活动而形成的一种对数量关系和空间形式的形式化知觉的能力。其中“形式化”是指把对象所共有的数学关系和联系用一般的形式结构表示出来。感知一些数学材料，好像具体数据、具体材料都消失了，剩下的仅仅是标志数学关系和联系的骨架。例如，对于诸如3+4=4+3、5+6=6+5、7+8=8+7等形式，能用a+b=b+a的形式来感知，而对具体的数字视而不见，这就是所谓知觉的形式化倾向。具有这种知觉的形式化倾向，是形成数学观察能力的重要标志。

2.发展分析比较能力

分析是比较的基础：为了确定不同事物的共同点，就需要把其中每一个事物分解为各个部分（或各个方面），分别研究其特征。比较是分析的继续和发展：把相应部分（或方面）的特征进行对比，确定它们哪些是相同的，哪些是不同的。分析比较能力是指通过数学活动形成的从各个局部（或各个侧面）对客观事物进行研究，并找出若干共同点和不同点的认识能力。即善于透过现象看到本质，善于抓住不同事物形式结构上的相同点与不同点。

例如，比较下列图形(www.xing528.com)

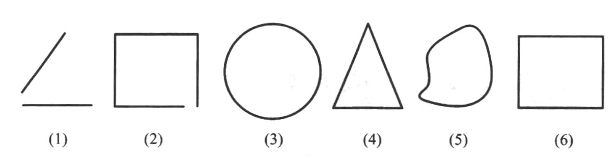
图10-2

这时可以从不同侧面加以认识。第一，它们都画在同一平面上，所以都是“平面图形”；第二，图形（1）、（2）不封闭，而图形（3）、（4）、（5）、（6）都是“封闭图形”；第三，图形（1）、（2）、（4）、（6）都是由线段构成，而（3）、（5）则都是由曲线构成；第四，图形（2）、（4）都有三个内角；等等。

3.发展抽象概括能力

抽象能力表现为善于归纳，把具有共同属性的事物看作一类，善于透过现象抓住本质，揭开表面上的差异性，发现隐藏在背后的共同特征的能力。概括能力表现为两个方面：一是把从特殊的具体事物中抽象出来的共同特征，推演到同类事物中，并形成一般概念的能力；二是从特殊和具体事物中，发现与某已知概念的关系，把个别特例纳入已知概念的能力。

例如，学生在观察、分析、比较的基础上，形成长方形表象，再从不同侧面认识它的特征：有四个角，四角都是直角；有四条边，两组对边分别平行且相等；有两条对角线，对角线相等。这就是抽象。把这些本质属性联合起来，并用词语“长方形”表示具有这些本质属性的一类事物，从这些本质属性中，筛选出能够限定长方形内涵与外延的本质特征，给出长方形概念的描述：“四个角都是直角的四边形”，这就是概括。保证抽象、概括能够顺利进行的学生的个性心理特征就是他们的抽象概括能力。

构建概念的数学思维能力的培养不是一蹴而就的，坚持下去，持之以恒，经过较长时间的努力，才会见到成效。不同学生构建概念的数学思维能力的发展也是不平衡的，在概念教学中既要照顾全体同学，又要因材施教，保证每一个同学都获得发展。

理解·反思·探究

1.什么是概念？什么是数学概念？

2.举例说明什么是概念的内涵与外延？概念的内涵与外延有什么关系？

3.小学数学概念具有哪些特点？为什么？

4.举例说明，概念形成、概念同化各经过哪几个阶段？

5.结合教学实际，谈谈概念引入的意义和作用以及概念引入的方法。

6.简述引导学生构建数学概念的基本策略。

7.结合教学实际，谈一谈你对发展学生构建概念的数学思维能力的做法与体会。

【注释】

[1]周玉仁.小学数学教学论.北京：中国人民大学出版社，1999.190

[2]克鲁捷茨基.中小学生数学能力心理学.上海：上海教育出版社，1988.110

[3]参见Heinrich Roth.教和学的教育心理学，德国汉斯·赛得尔基金会和上海师资培训中心联合编印，12