思维就是人类揭示事物本质特征的过程,而数学就是研究存在的和思想的现实或关系本质的科学。因此,数学学习的过程首先就是思维的过程。儿童对现实世界的观察,对观察对象的分类与比较,对事物属性的归纳与抽象,对性质和规律的运用等等,都是思维的过程。人通过深入的思考而获得对数学的理解,通过深入的思考获得数学素养。人的数感、数学观念、数学思想、数学运用能力等都是在数学思维过程中形成与发展的。
可见,学习数学,不仅因为数学是个体在社会生活中有用的工具,更重要的,数学还可以促进人的思考,即数学是促进个体思维素质发展的重要基础。今天的人需要更精确地去了解和解释世界,需要能更主动、更有效地与人沟通,需要更具创造性的生活,而所有这些,都需要有敏锐的和创造性的思维能力。因此,用数学眼光看待世界并有意识且适当地运用数理思维,是一种重要的素养。
当然,儿童尚处在以具体的形象思维为主,并逐步向抽象的逻辑思维过渡的年龄阶段。低年级儿童更多的是具体的形象思维,到了中高年级,抽象逻辑思维的成分逐渐加大,但一般还不能完全依靠抽象的数学概念进行思考,往往还需要具体的形象思维的支持。因此,发展儿童的数学思维能力,必须遵循儿童的认知规律。
(一)观察与比较
1.观察
所谓观察,就是指人们对周围客观世界的各个事物和现象,在其自然条件下,按照客观事物本身存在的自然联系的实际情况,加以有目的的感知,从而来确定或研究它们的性质或关系的一种思维活动。观察是多种感觉器官对对象的有意识的知觉。观察具有这样两个特征:
第一,观察的双重性。即观察不仅仅是指利用各种感觉器官对客观事物进行看、触、听、嗅、尝等感知活动,还包括对客观事物的领会和理解。例如,儿童在学习长方形面积的计算时,可能先观察由若干单位面积的小正方形组成的长方形,然后用数数的方式得出该长方形的面积。这时就会引起他们思考,长方形的面积都要通过“数”吗?面积与长方形的哪些要素有关系呢?接着就会进一步地观察,在这个长方形中每一排有几个这样的小正方形,共有几排。于是,又引起他们深入思考,这样的每排几个和有这样的几排,与长方形的面积有什么关系呢?显然,在整个观察活动中,感知和思维是同步进行,互为条件的,感知为思维提供了依据,思维又为进一步感知提供了新的目标。可见,观察的根本目的就是为了发现问题和找到反映事物本质的规律,因此学会思考性地观察很重要。
第二,观察的客观性。格式塔(Gestalt)曾做过这样的实验,当人们在感知诸如图1-1所示的图形时,总会在知觉中自觉地将它们看做是三角形、正方形和圆,即人的知觉有一种趋向于稳定性、完整性和对称性的倾向,这就是观察的主观性。要保证观察的客观性,就需要掌握一定的观察方法。通常从观察顺序看,主要有:整体→部分→整体和部分→整体→部分这两种方法。而方法的选择主要取决于在数学学习中观察的任务和对象的特点。
从儿童的思维发展特征看,他们观察能力的发展有较为明显的阶梯性,即:对象的概括化能力→知觉的形式化能力→空间结构的知觉能力→逻辑模式的识别能力。
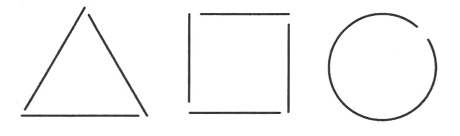
图1-1
2.比较
而所谓比较,实际上它是借以认出对象和现象的一种逻辑方法。在数学学习中,利用比较,可以形成新的概念,例如,通过比较自然数的约数的性质,可以认识质数与合数;利用比较也可以区别相近或相似的概念,例如,通过比较,可以区分除尽与整除的关系,或者区别竖直与垂直的不同;利用比较,还可以形成比较自身的概念,例如,通过一一对应的方式,可以形成“多和少”或“长和短”等比较的概念。对小学生来说,发展他们的比较能力,要注意其阶段性。
首先,引导儿童先比较事物的不同因素,再发展到比较事物的相同因素。其次,引导儿童先比较事物差异性较大的属性,再发展到比较事物差异性较小的属性。最后,要遵循从感知比较发展到表象比较,再发展到概念比较这一规律。
(二)分析与综合
分析和综合是人类认识事物本质的必不可少的基本思维过程。数学知识是客观事物的抽象的和模型化的反映。因此,能否将概念还原成事实,要看概念掌握的清晰程度和深刻性,这就要依赖学生的分析与综合能力。所谓分析,简单地说,就是指在头脑中将对象和现象分解成个别部分,从中找出它的属性、特征等,单独来考察的思维活动,而所谓综合,就是指将分析了的各个部分结合起来,从整体来考察对象或现象的思维活动。
分析始于感知,但它属于一种片面感知,不能获得整体认识。综合则是将片面的感知进行整合,形成整体知觉。一般说来,没有分析就谈不上综合,但分析并非一定在综合之前。同时,分析和综合是伴随在同一认识活动过程之中的。
儿童的分析、综合能力,有一个从低级阶段到高级阶段的发展过程。所谓低级阶段,即指分析和综合是与感知觉直接挂钩的;而所谓高级阶段,则是指分析和综合不再与感知觉直接挂钩。(https://www.xing528.com)
在小学数学学习中,可以利用多种途径对儿童进行分析与综合能力的培养,如:
利用某些问题解决学习来发展儿童的分析与综合能力。因为在问题解决学习过程中,有一个理解问题的活动,而这一活动就是在头脑中构造问题表征的活动。这是一个不容忽视的阶段。研究表明,许多问题解决的障碍可能并不在于问题解决的策略不当或者过程有误,而往往在于对问题性质的认识与问题表征存在某些问题。一般来说,问题从被确认到获得解决,有一系列不断变化的状态,即从问题的起始状态到问题的目标状态,首先就有一个表征构造的过程,而这一过程就是一个不断分析与综合的过程。只有这样,才能从问题的起始状态出发,通过图式的检索进入并逐渐逼近问题的目标状态。
利用某些计算(规则)学习来发展儿童的分析与综合能力。仅从计算的审题过程看,儿童除了往往表现出对题目审题不重视外,还表现出审题无顺序、粗糙和随意性强等特点,从而影响解题的正确性或速度。
(三)抽象与概括
抽象与概括也是人类认识事物本质的一个必不可少的基本思维过程。所谓抽象,简单地说,就是指发现事物的本质属性,放弃非本质属性的思维过程。所谓概括,简单地说,就是指从个别单独的属性,推广到同类事物的属性的思维过程。
数学学习的过程就是培养抽象与概括能力的过程,这首先是由数学科学本身的抽象性特征所决定的。其次,数学科学是对客观世界的本质属性最一般的反映,而这种最一般的反映必须要以抽象为前提。但是,由于儿童尚处于以具体形象思维为主并逐步向抽象逻辑思维过渡的年龄阶段,其内部的思维活动就需要有一定的外部支撑点——直观的感知。因此,对儿童的抽象与概括能力的培养,应注意要有一定的阶段性。
按皮亚杰等人的研究,低年级的儿童尚处在“前运算阶段”(相当于布鲁纳的“动作式阶段”)向“具体运算阶段”过渡阶段,往往只能形成“一级概念”(具体概念),而要形成“二级概念”(定义概念)还比较困难。他们往往只能依赖经验(直观)进行初步的抽象,而这种抽象与概括的发展是依据对象的外显的特征入手的分类开始,凭借感觉学习来形成和保持各种表象,也就是说,他们的概念还往往依赖直观或经验来支撑。
而年龄稍大一些的儿童开始处于“具体运算阶段”(相当于布鲁纳的“映象式阶段”),守恒概念逐渐形成,而且思维的可逆性和多维性逐渐得到了发展,能将环境中的经验构成内在的表象,并开始能摆脱分类而从事物的内部特征入手,从而可能获得一些“二级概念”。但是,这个阶段的儿童在获得和适用这些概念的时候,仍需一定的直观形象来支持。
到了更高些年龄段的儿童,他们的思维水平已开始从“具体运算阶段”向“形式运算阶段”(相当于布鲁纳的“符号式阶段”)过渡,他们已有一定的将抽象的假设或命题进行逻辑转换的水平,开始能用符号进行思维,而且概括能力也开始增强,能将一类本质属性推广到同类事物中去。
例如,对“角”的认识,低年级的儿童,可能只能从日常的经验或活动的体验来获得,因而在他们看来,角是“尖”的,还不能形成对图形特征的表征;稍高年级的儿童,可能就会从图形特征入手,从了解图形的基本组成去形成对图形的表征。但是,对于图1-2所示的图形,他们可能就会糊涂,这究竟是“勾”还是“角”?更高年级的儿童,可能就会从“角”的发生角度去真正理解其本质含义,并开始懂得对情境对象依照一定的规则做符号推演(判定)。
![]()
图1-2
(四)判断与推理
判断与推理也是最基本的和主要的思维过程。所谓判断,就是一个由理解(概念)到结论(概念)的思维过程,它是反映事物和现象某些本质属性的思维过程。在数学中,命题常常是判断的一个重要的形式,它是数学问题解决的重要的思维工具。
而所谓的推理,就是从一种判断作出另一种判断的思维过程。它通常可以分为归纳推理、演绎推理和类比推理三种不同的形式。
直觉作用大、判断受经验的干扰以及概念不清是儿童在判断过程中常表现出来的一些特点,例如,“哥哥有10本书,弟弟有6本书,哥哥给弟弟几本书,两人就同样多?”儿童凭借直觉就会认为,将哥哥比弟弟多的部分给弟弟后。两人就同样多了。因此,首先可以通过加强概念教学来发展儿童的判断能力。因为判断是由概念组成的,而且概念的形成与概括本身就是一个判断的过程。其次,可以通过让儿童反思自己的学习过程来发展简单的判断能力。总的来说,培养儿童在数学的表述与交流中能言而有据、基于以准确的概念来反思自己的学习是发展他们判断能力的最有效的途径。
发展儿童的推理能力也是一项重要的任务。一般说来,在小学数学的学习中,往往较多的是采用“不完全归纳”的推理,即从直观出发,让儿童利用观察、操作、比较,获得感知体验,从而在分析、抽象的基础上获得认知。
但对年龄稍低的儿童来说,他们对抽象的假设或命题进行逻辑转换的思维能力尚未真正形成,往往较难认识到一个判断与另一个判断之间的逻辑关系,因此,虽然演绎思维有利于培养学生言而有据的科学态度以及判断合乎逻辑的思维品质,但在具体的运用中,通常需要从最简单的因果关系入手,以“因为……所以”这种直接演绎的方式来表述自己的观点或想法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




