19世纪数学的另一伟大成就,是高等代数的开创性进展。
代数学的主要内容之一是求解代数方程和代数方程组。
早在古代数学的发展中,数学家们就发现了一次、二次、三次、四次代数方程的根式求解法。后来数学家们开始向五次和五次以上的高次代数方程进军,力图用同样的方法求解高次代数方程。在这个过程中,开创了一个新的数学分支——群论。
在对高次方程的根式求解中,做出杰出贡献的是两位不到30岁的年轻数学家阿贝尔和伽罗华。
阿贝尔是挪威人,于1802年8月5日出生在克里斯卡尼亚附近的一个贫苦乡村牧师的家庭里,幼年丧父。由于家里生活非常困难,使阿贝尔不能按部就班地求学深造。
阿贝尔自幼聪明好学,数学成绩出众,因家境贫寒,常常依靠周围的人和亲友的帮助,使他在求学时期就结交了许多朋友。
从中学时代起,阿贝尔对数学更感兴趣,这和学校的数学教师霍伦波很有关系。霍伦波有较高的数学知识,对班级的数学尖子阿贝尔非常喜欢,注意培养他的数学才能,发掘他的数学天赋,借给他数学家的名著。
从此,阿贝尔一头扎进数学家的著作里,刻苦攻读,成了“数学迷”。中学还没有毕业,阿贝尔就向当时公认的数学难题,关于五次方程的代数解法展开了进攻。
我们知道一元一次方程的求根公式,也了解一元二次方程的两个根的求根公式。
比如在二次方程ax2+bx+c=0,其中x是未知数,a,b,C都是已知数,那么这个二次方程的根可用公式: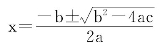 来计算。
来计算。
凡是给出这样一个公式的,就把方程称为“可以代数求解”,凡是给不出这样一个公式的,就把方程称为“不可以代数求解”。
二次方程的代数解法,很早就解决了。三次、四次方程的代数解法,已在16世纪由意大利数学家塔塔里亚和费拉利等人解决了。
数学家的目光自然地转移到五次方程或更高次方程的求根公式上。在17世纪和18世纪,几乎所有数学家都研究过这个问题,但都没有成功。著名数学家欧拉和拉格朗日也研究过这个问题,拉格朗日说,这个问题好像是在向人类的智慧挑战。
既然许多人的尝试都失败了,是否像欧氏几何中的第5公设不可证明一样,根本不存在四次以上高次方程的代数解法呢?但是,这也需要数学证明。1801年,高斯在他的《算术研究》一书中指出,某些高次代数方程能够用根式法求解。但是,他没有进行严格的证明。
阿贝尔在中学就向这个难题进军,充分发现了他初生牛犊不怕虎的闯劲,以及青年人那敢想敢干的蓬勃朝气。当然,他的努力失败了,毕竟他还太小,掌握的数学知识太少,单凭朝气和闯劲是解决不了问题的。
1820年,阿贝尔在亲友的帮助和支持下,考入大学。当时,这所大学没有数学系,而阿贝尔的特长在数学方面,于是他在完成学校规定的课程外。把全部时间和精力用于研究数学。
在大学期间,阿贝尔继续研究五次方程的求解问题。怎样用加、减、乘、除和开方的代数运算,来求出五次方程的解呢?他冥思苦想,反复运算,希望有朝一日能解决这个难题。
阿贝尔善于学习前人的经验,特别对一些数学大师的著作深有研究。欧拉、拉格朗日、柯西、高斯等人的著作和文章,都对阿贝尔很有启发。通过不断的探索和研究,在1824年,22岁的阿贝尔根据意大利数学家鲁芬尼的预言,证明了五次代数方程用加、减、乘、除、开方等代数运算将根明显地表达出来是不可能的。(https://www.xing528.com)
在此基础上,阿贝尔写成论文《论代数方程,证明一般五次方程的不可解性》,从而解决了几百年一直没有解决的问题,开辟了近代代数方程论的道路。这篇论文,以后被收进阿贝尔的全集,流传至今。
但在当时,阿贝尔必须自己掏钱来印刷论文。贫穷的阿贝尔读书都要别人资助,哪里有钱呢?阿贝尔深知这一结果的重要性,为了让更多的人知道,便咬紧牙关,把论文浓缩成只有6页的小册子,印刷了出来。可惜的是,由于论文太短,他的证明就显得不够充分了。
阿贝尔满怀信心地把这些小册子寄给外国一些著名的数学家,希望得到他们的肯定。
但是,阿贝尔没有想到,一个22岁的不知名的小人物,解决了几百年悬而未决的大问题,这能叫人相信吗?当那些数学权威们收到他那印得很差的论文时,有的人随手翻了一下便扔进了垃圾堆,甚至有人连翻都没有翻,就弃之一边了。
当数学之王高斯收到小册子时,觉得用如此短的篇幅来证明这个著名的问题是不可能的,便随手放进了书堆里。他哪里知道,这个小册子是阿贝尔无钱出版而高度浓缩的呢?
大学毕业后,阿贝尔为了得到名家指点,钻研自己喜爱的数学,在1825年来到德国柏林。由于找不到工作,只得靠投稿加做工来维持生活。但不管遇到什么困难,他都离不开数学,而是仍然按照他的计划和目标向数学王国冲锋陷阵。
阿贝尔是一个意志非常坚强的人,他钻研数学的目的,不是为了金钱,也不是为了出人头地,更不是为了成名成家,而是为了科学。即使再极端的困难,甚至在连肚子都填不饱的情况下,他仍然没有放弃数学研究,而是信心十足地探讨数学问题。1826年,阿贝尔到了法国。他把写成的长篇论文《论一个非常宽广的超越函数族》,托人转交给大数学家柯西,直到年底一直音讯杳然。
由于阿贝尔在国外受到冷遇和歧视,生活又没有保证,1827年,他只好回到挪威。回国并不意味着生活有了保障,等待他的仍然是穷困潦倒。
不久,阿贝尔在朋友的帮助下,到一所军事学院代课,生活稍有改善。由于贫穷就像老朋友一样始终没有离开过他,已经把他的身体折磨得越来越虚弱了,生命留给他的时间已经很少了。
阿贝尔抓紧最后的时间,拼命研究数学,又取得了一些成就。
1829年4月6日,这位年仅27岁的青年教学家逝世。
在阿贝尔短暂的一生中,他在数学的许多方面都取得了很有创见的成就。
首要的成就是,证明了五次方程不可能用一般数学方法求解,震动了整个数学界。
其次是彻底证明了二项式定理。
再次是创立了椭圆函数论,等等。
如果大数学家高斯、柯西等人在认真地看过阿贝尔的杰出论文后,为他说上一句话,就会使他摆脱贫困,而不至于英年早逝,那么阿贝尔将不知道要解决多少数学难题,数学发展的步伐就会大大加快。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




