在经典三方博弈中,有一个搅局者(spoiler)模型。所谓搅局者,是指自己地位较低或实力较弱,在另外两强竞争之间不可能获胜却可能阻止其他人获胜的参与者。美国作为当今世界唯一超级大国,实力强大,但是在亚太地区,虽有强大影响力,但是毕竟中国、东盟国家地缘上更接近,另外这里主要考虑中国东盟国家的关系,于是考虑美国作为三方博弈中的搅局者。
经典搅局者模型的例子是2000 年美国大选中的纳德、戈尔和布什的博弈。在四个候选人中,共和党的布什和民主党的戈尔是真正旗鼓相当的竞争者。民意测验表明,他们的支持率几乎不相上下。改良党的布坎南无足轻重,但是绿党的纳德却有一定的号召力,他成了戈尔的隐患,充当了该博弈中的搅局者。
对这次大选中的三方博弈标准型可以表示为如图5 所示:
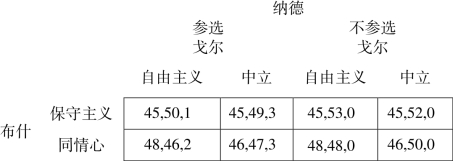
图6 2000 年美国总统大选博弈
各参与者的收益用获得的普选票数表示。戈尔的参选存在的不利因素是,他获得的普选票数必须超出其他竞选者1%才有机会赢得大选。当然,获得的普选票数越多,候选人在后续的选举中地位就越有利。(https://www.xing528.com)
在该博弈中,对纳德而言,参选是优势策略。布什也存在优势策略,同情心。戈尔没有优势策略。
该博弈的纳什均衡是(同情心,中立,参选),收益为(46,47,3)。
实际上,美国、中国无论在政治、经济、军事等各方面都在世界上处于领先地位,而东盟虽然集中了东南亚10 国力量,却还是无法与中美对抗。可以考虑在没有美国加入时本质上是一个东盟搭便车模型,而有美国参与时,会改变博弈收益情况。于是,考虑这个特殊博弈中两强一弱(中美强东盟弱)或者两弱一强(中国强,东盟弱,美国在地理上远离东南亚地区,影响力弱)的实际情况,有三方博弈标准型可以表示为如图7 所示:
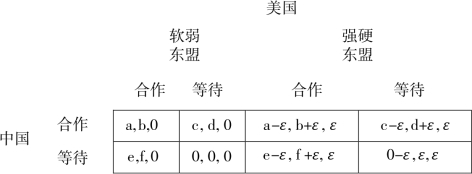
图7 考虑中美强、东盟弱的三方博弈
该博弈中,美方采取强硬策略的收益εi >0,i = 1,2,3,4。至于在美方该策略下,东盟的收益不同于经典的搅局者模型,实际上东盟在大国平衡战略之下的收益是普遍增加的。而中国的收益应该普遍有所减低。虽然东盟的增量,中国的减量与美国的收益不尽相同,但差异不至于影响策略的选取,为表达方便,各方收益如图7 所示。这样,该博弈的纳什均衡是(C,W,H),也就是中国主动寻求与东盟合作,东盟等待,美国力求影响两者的合作,东盟由此收益增加,中国收益降低。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




