由于政府禁止公开吸储所带来的人们对企业吸储预期的改变,工厂商号吸储的能力受到限制,即K′有所下降。同时,政府对退职金的要求,使资方对管理权重视,进而使管理回报r呈上升趋势。随着K′下降、r增加,职工储蓄为“保障”的收益Kr增加,职工储蓄为“融资”的收益K′r′下降。当变化到一定程度时,会出现:Kr>K′r′>Kr-C。根据图4.1表示的博弈,这时会有两个纯策略纳什均衡,即每家企业都选择举办职工储蓄为“融资”的目的(融资,融资),或每家企业办理职工储蓄都是为了“保障”的目的(保障,保障)。从博弈矩阵本身分析,(保障,保障)的博弈均衡更加有效,因为这时双方企业的收益都要更大。但根据博弈的演化分析可知,虽然两个均衡都存在,但由于均衡锁定,前期均衡结果会影响后来的均衡结果。在本文的博弈中,表现在(融资,融资)由于是前期的均衡结果,在没有巨大的外部冲击下依然会成为后来的均衡结果,虽然并不是有效的均衡结果。具体的分析如下:
对博弈的演化分析,即演化稳定策略(ESS)的求解。演化稳定策略是建立在纳什均衡之上,并且是能够抵御变异的策略,这种变异来自博弈方的偶然出错、模仿等。根据Cressman(1997)[46]的证明和复制动态方程可知图4.1所示的博弈矩阵的演化稳定策略为F和S[47],即两个纯策略纳什均衡都是演化稳定均衡。但问题在于基于演化起点会产生均衡锁定。如图4.2所示,B点代表都选择策略S(保障)为目的的均衡,C点代表都选择F(融资)为目的的均衡,A点则代表图4.1博弈的混合策略纳什均衡。即在A点,博弈方以P的概率采取策略F,并以1-P的概率采取策略N,这时博弈方采取任何策略的期望效用都是相同的,即U(S)=U(F),如果这时采取策略F的比例为P*,那么P*可以表示为:
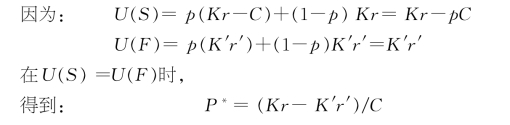
 (https://www.xing528.com)
(https://www.xing528.com)
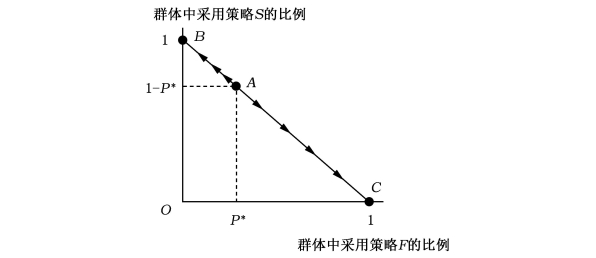
图4.2 动态演化相位图
在P*所在的A点,演化的动力过程如箭头所示。当初始点位于A点右边时,即群体中采取战略F的比例大于p*时,U(S)<U(F),根据适者生存的规则,会有更多人选择策略F,群体演化的结果会是都以“融资”为目的。从长期来看,这种均衡具有锁定(lock in)的特征,即使有一部分企业选择以“保障”为目的,却无法改变整体均衡的最终结果是“融资”。在锁定状态下,只有外生的巨大冲击才能跳过A点,至A的左上方,并达到另一个均衡。这种冲击可以来自政府也可以来自自然。另外,企业职工储蓄“融资”行为给“保障”企业带来的成本C会影响分界点A,C越大A点越靠近B点,这时均衡策略(F,F)越难以逃离。
根据演化博弈的分析结果可知,虽然“保障”的均衡更有效,但由于演化均衡的锁定特征,均衡结果难以被打破。具体表现为职工储蓄的目的,在20年代末30年代初,未见有整体性的变化:没有更多的企业设立以“保障”为目的的职工储蓄。[48]有效均衡的无法达到为政府干预提供了空间。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




