趋势线示例和分析：对数、线性和多项式拟合优劣分析

1.线性趋势线

线性趋势线使用线性回归模型描述变量关系。图5-36是一个添加线性趋势线后的XY散点图，趋势线设置中选择了“显示公式”和“显示R平方值”，拟合后的趋势线方程为Y=4.2827x-122.78，R平方值0.6095。

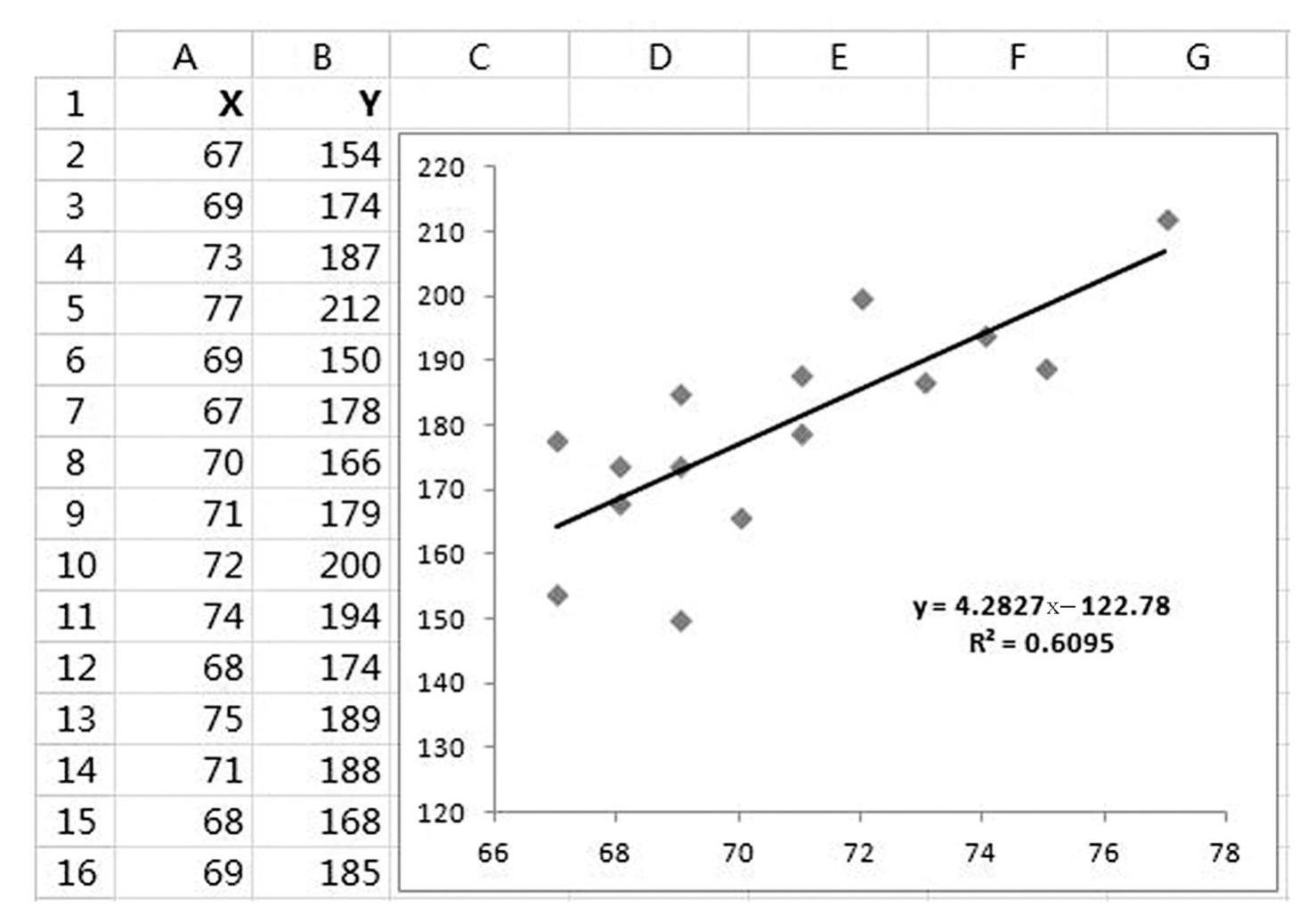
图5-36 线性趋势线

一元线性回归模型的一般形式为y=a+b∗x，其中，a代表截距，即拟合线和y轴相交的点，斜率代表每单位x的变化导致的y的变动幅度。R平方也称为决定系数，取值范围从0到1，衡量趋势线的估计值和实际数据的接近程度，即趋势线的拟合优度。R平方的值越高，则说明趋势线越可靠，如所有数据点都落于趋势线上，则R平方为1。

趋势线公式可用于数据预测，由于参数a和b已知，给定一个x值，即可计算y的预测值。例如当x=67时，预测的y=4.2827∗67-122.78=164.16。

2.对数趋势线

对数趋势线较适用于在形态上和对数曲线相似的数据：在快速上升或下降之后总体趋势趋于平坦。对数回归模型形式为：y=c+b∗ln（x）。下图采用了对数趋势线，显示的公式和R平方分别为：

y=25.551ln（x）+12.007

R=0.9549

作为对比，本例如使用线性趋势线，则拟合R平方值仅为0.7656，说明根据绘图数据的特征采用对数趋势线能够大幅度改进拟合水平。

根据对数趋势线模型可以看出，如将对数趋势线绘制在对数X轴的刻度即ln（x）上，其效果将是一条直线，等同于线性趋势线（见图5-37）。

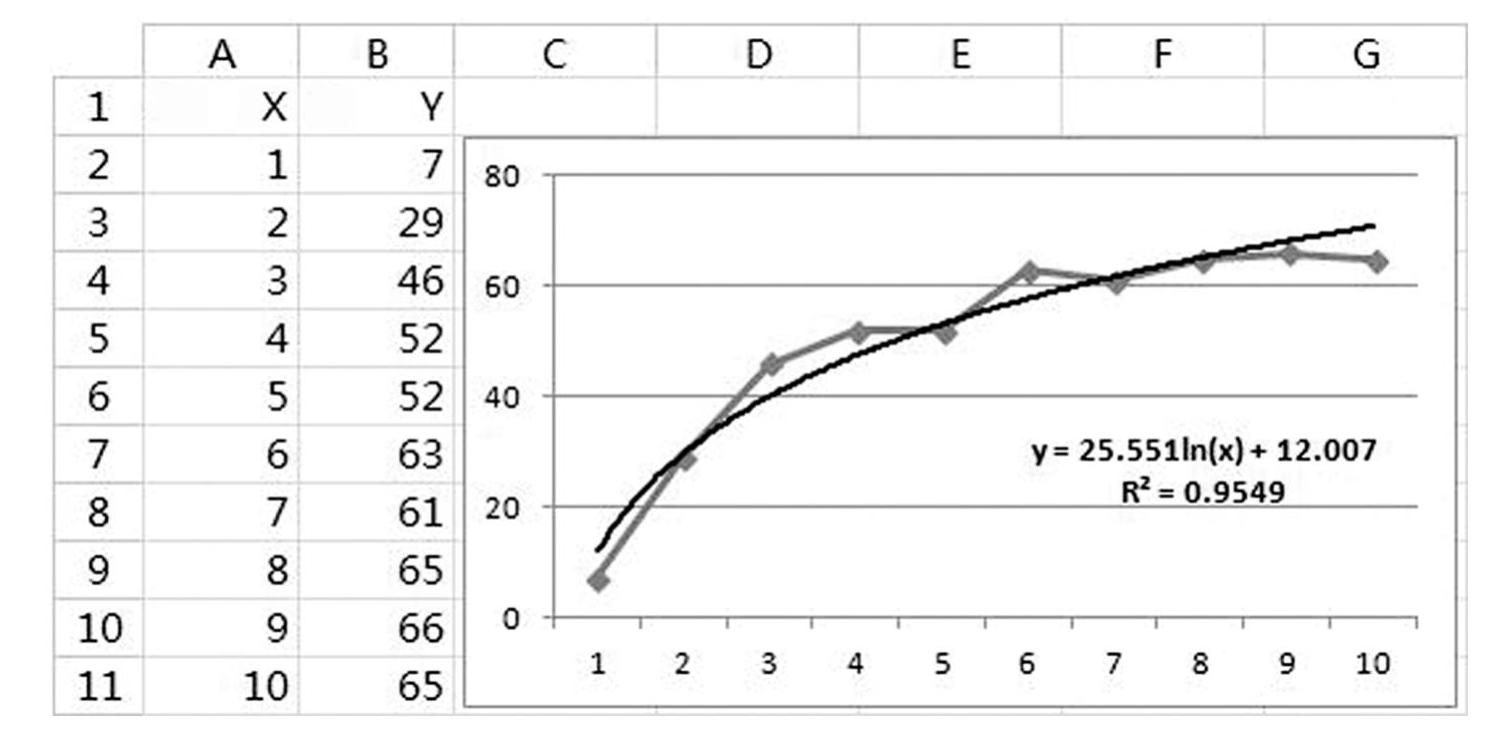
图5-37 对数趋势线

3.乘幂趋势线

乘幂趋势线主要用于描述按某一特定速率上升或下降的数据，其模型形式为：y=a∗（x^b），两边取对数后变成ln（y）=ln（a）+b∗ln（x），因此，乘幂模型也称为双对数模型。显然，在对数x轴和对数y轴刻度上，乘幂趋势线将是一条直线。下例中的散点图采用了乘幂趋势线，显示的公式和R平方分别为：

y=6.6666x^2.4387

R²=0.9749

本例如采用线性模型，R平方将降至86%，说明绘图数据更适合使用双对数模型（见图5-38）。需注意的是，在双对数模型中，x只能为正数，因此包含零或负数的绘图数据无法创建乘幂趋势线。(www.xing528.com)

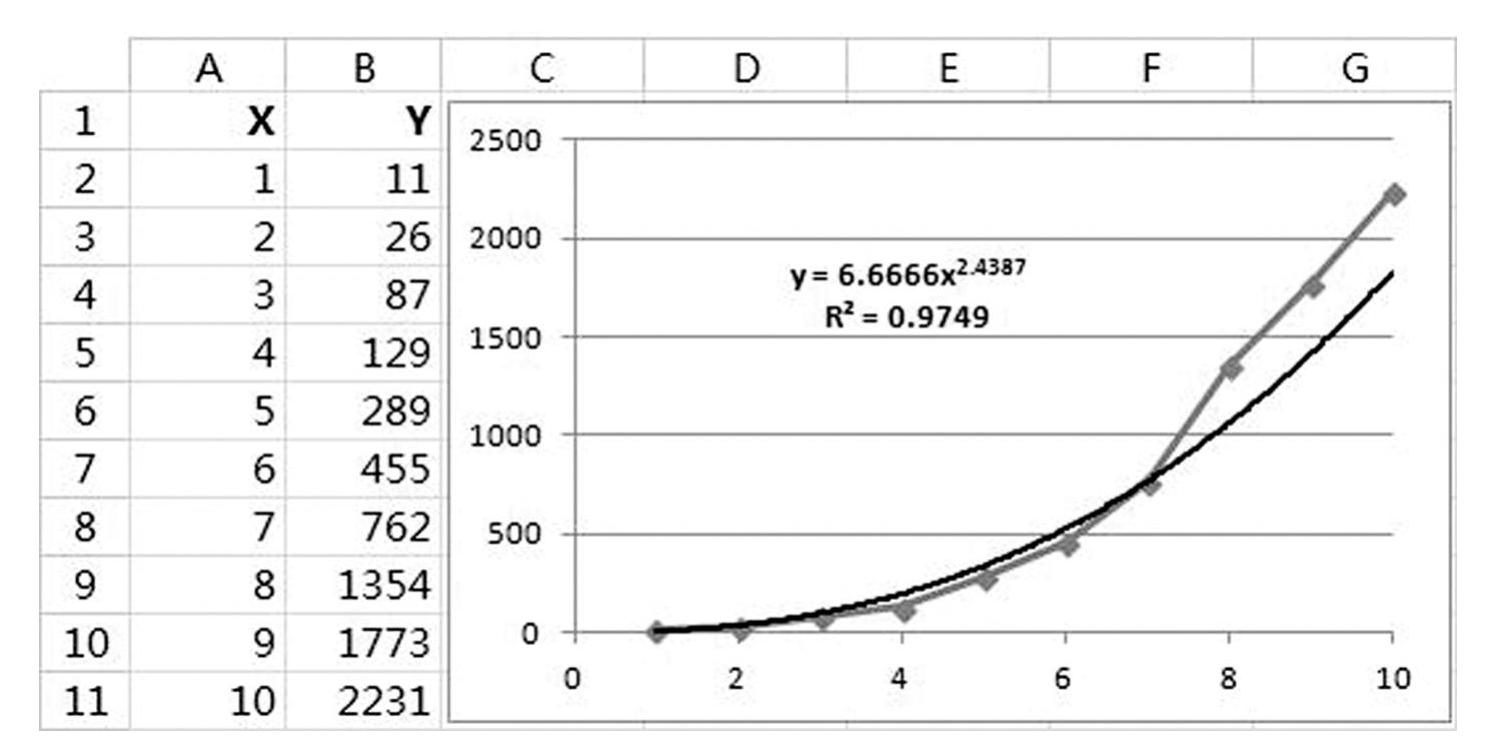
图5-38 乘幂趋势线

4.指数趋势线

指数趋势线适用于增减速度不断加快的绘图数据，其模型形式为：y=a∗exp（bx），两边取对数后变成ln（y）=ln（a）+b∗x，因此，指数模型也称为对数-线性模型。显然，在线性x轴和对数y轴刻度上，指数趋势线将是一条直线。和乘幂模型相同，包含零或负数的绘图数据无法创建指数趋势线（见图5-39）。下例采用了指数趋势线，显示的公式和R平方分别为：

y=10.718e^0.6207x

R²=0.9685

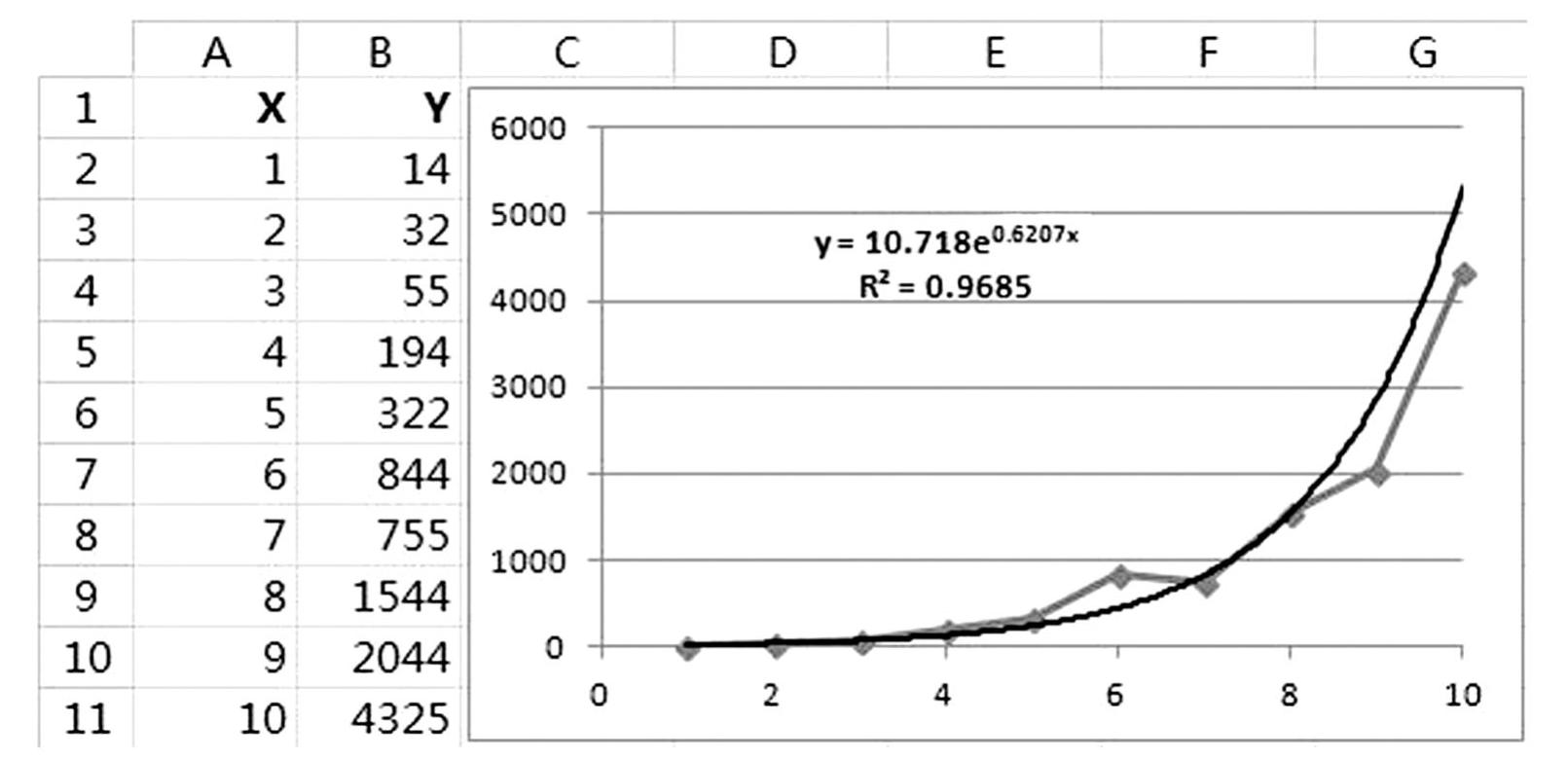
图5-39 指数趋势线

5.多项式趋势线

多项式趋势线适用于波动较大且有规律的数据，模型形式为：y=a+b∗x+c∗x^2+d∗x^3+…。

使用多项式趋势线需同时指定其阶数，多项式模型的阶数可由数据波动次数或拐点个数确定，Excel支持的多项式阶数介于2至6之间（见图5-40）。下例采用了二阶多项式趋势线，显示的公式和R平方分别为：

y=63.462x²-725.25x+2731.7

R²=0.8479

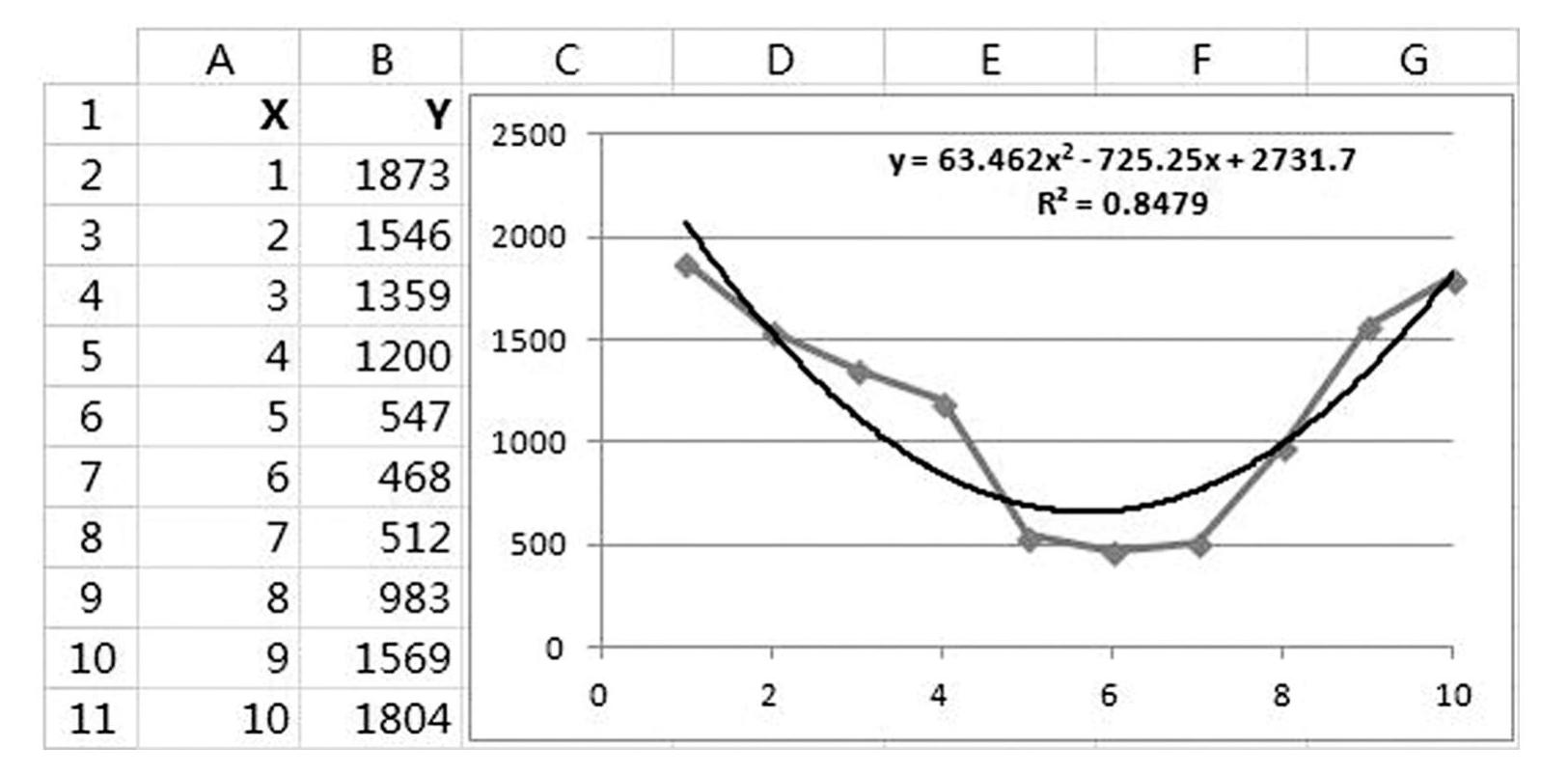
图5-40 多项式趋势线

6.移动平均线

移动平均线本质上并非数据趋势线，而是对原始数据的一种平滑处理。移动平均计算由“周期”选项决定的特定数量的原始数据点的平均值，并将此平均值作为趋势线上的数据点。例如，如“周期”设置为2，趋势线的第一个数据点是原始数据中第一个和第二个数据点的平均值，即Excel对每相邻两个原始数据点求平均，以获得趋势线上的一个数据点，因此对于2期移动平均线，数据点总数较原始数据点数量少1。随着周期数的增加，移动平均线会趋于平滑，但损失的数据点也会相应增加。