在“3.3.1.2 PE-ROE独立分组回报结果”一节中，笔者对ROE、PE构建的投资组合采用算数平均回报率，证明了H2假设；在“4.1.2 PE-ROE的加权平均检验”一节中，笔者又采用加权平均回报率对假设H2进行了稳健性证明。
在本小节，笔者将进一步对ROE、PE采用非独立分组计算回报率的方法，再次对假设H2进行稳健性检验。
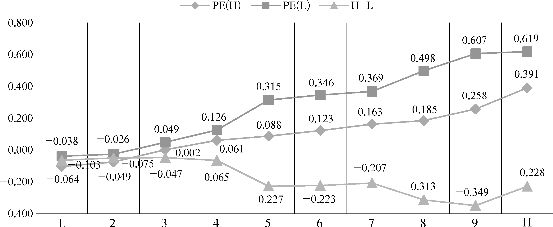
附表20展示了按照ROE和清单所展示变量PE分组建立投资组合所得到的回报率结果。在每个起始年份，按照每个Δt年限，首先按照ROE分为10组，然后在每个ROE的分组内将清单所列变量PE分为10组，从而得到10×10共100个投资组合，计算得到每个投资组合的算数平均回报率，并计算按照各个初始年份得到的投资组合的回报率的总体均值。
根据附表20的数据结果，我们整体分析ROE、PE非独立分组对股票收益产生的影响。
（1）无论当Δt＝1年、5年、10年还是20年，PE（H-L）各组整体具有较好的显著性。
（2）在相同ROE分组内，低PE相对高PE的股票收益更大。
（3）无论是PE（L）组还是PE（H）组，随着ROE分组从低到高，股票收益也随之升高，这主要是ROE变量对投资组合的贡献。
（4）在显著性前提下，H-L均为负值，也就是PE与投资组合的收益呈负相关。
以上（1）—（4）点，可以在每一个周期的图形中体现，如图4-17、图4-18、图4-19、图4-20所示。
(www.xing528.com)
图4-17 ROE-PE非独立分组算术平均收益（Δt＝1年）
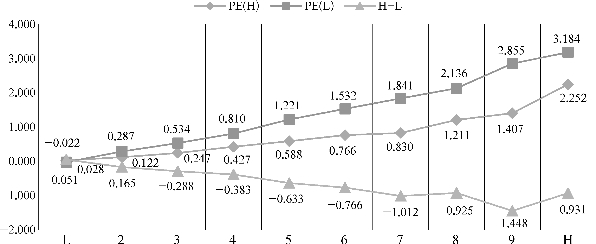
图4-18 ROE-PE非独立分组算术平均收益（Δt＝5年）
图4-19 ROE-PE非独立分组算术平均收益（Δt＝10年）
图4-20 ROE-PE非独立分组算术平均收益（Δt＝20年）
因此，在本小节，笔者通过对ROE、PE构建的非独立投资组合，再次有效地对前文结果进行了稳健性检验。假设H2稳健性检验满足。
H2：在ROE相同分组内，市盈率（PE）因素对股票收益呈负相关，低市盈率比高市盈率的股票收益更大。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
