在“3.3.2 变量回归结果检验”一节中,笔者对投资组合的算数平均回报率按照ROE、PB、PE依次进行回归,H5假设获得了显著性证明。
在本小节,笔者将进一步对投资组合的加权平均回报率按照ROE、PB、PE依次进行回归,检验其结果是否同样具有显著性。
Coefficient=1、5、10、20分别代表构造投资组合所选取的区间年限长度,组合内每只股票的权重为该股票市值占投资组合全部市值的比值。
对每一个自变量,对应数据的第一行为该变量回归系数,第二行表示回归系数的T值。Intercept为截距。
接下来,笔者将逐一分析Δt=1、5、10、20年时的回归结果。
1.Δt=1年的加权平均回归结果
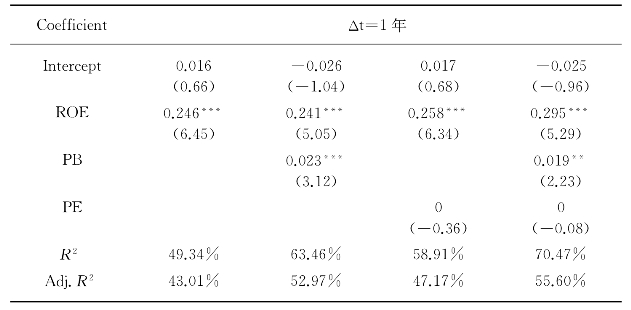
根据表4-2可以看出,当Δt=1年期时,ROE的回归结果在1%水平上显著;在ROE/PB两因素的回归方程中,PB在1%水平上显著,在ROE/PB/PE三因素的回归方程中,PB为5%显著。但回归方程中,PE不显著。
表4-2 加权平均回归结果(Δt=1年)
注:***、**、*分别表示在1%、5%和10%统计水平上显著。
同时,可以看出,1年期的股票收益,来自ROE单一因素的解释力度为49.34%;ROE、PB两个因素共同作用,解释力度为63.46%,比单一ROE因素的解释力度增加14.12%。
若ROE、PE两个因素共同作用,解释力度为58.91%,比单一ROE因素的解释力度仅增加9.57%,可见PE因素的影响小于PB因素的影响。
若ROE、PB、PE三个因素共同作用,则对股票收益来源的解释力度达到70.47%,比单一ROE因素的解释力度增加21.13%,比ROE、PB两个因素的解释力度仅增加7.01%,可见ROE、PB两个因素基本决定了一年期股票的收益,而且ROE是最核心的因素,解释力度接近50%。
而且,通过表4-2可以得到基于ROE、PB、PE三个因素依次进行回归的1年期回归方程。
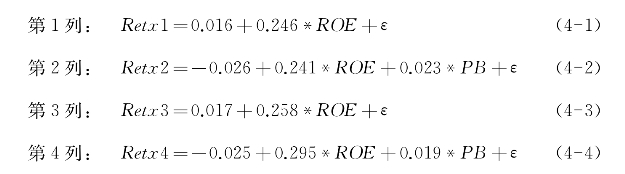
从截距项(intercept)来看,式4-1、式4-2、式4-3、式4-4四个回归方程的截距项的解释力度均不显著。
2.Δt=5年的加权平均回归结果
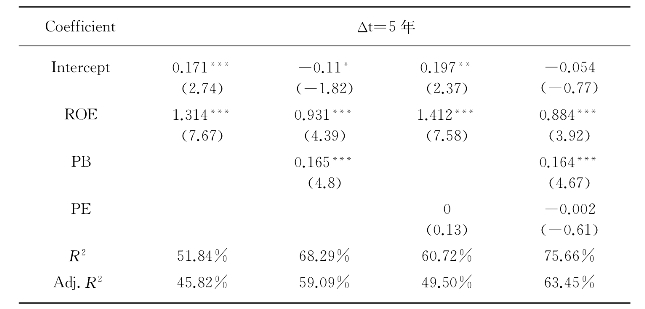
根据表4-3可以看出,当Δt=5年期时,ROE、PB的回归结果在1%水平上显著,但PE不显著。
表4-3 加权平均回归结果(Δt=5年)
注:***、**、*分别表示在1%、5%和10%统计水平上显著。
同时可以看出,5年期的股票收益,来自ROE单一因素的解释力度为51.84%;ROE、PB两个因素共同作用,解释力度为68.29%,比单一ROE因素的解释力度增加16.45%。
但是,若ROE、PE两个因素共同作用,解释力度为60.72%,比单一ROE因素的解释力度仅增加8.88%,可见PE因素的影响小于PB因素的影响。
若ROE、PB、PE三个因素共同作用,则对股票收益来源的解释力度为75.66%,比单一ROE因素的解释力度增加23.82%,比ROE、PB两个因素的解释力度增加7.37%,可见ROE、PB两个因素基本决定了五年期股票的收益,而且ROE是最核心的因素,解释力度超过50%。
而且,通过表4-3可以得到基于ROE、PB、PE三个因素依次进行回归的5年期回归方程。
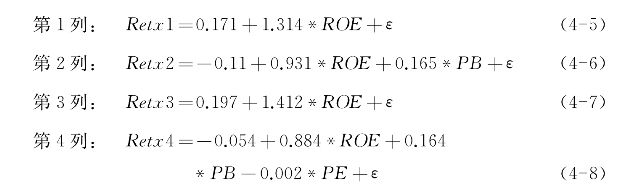
从截距项(intercept)来看,式4-5、式4-6、式4-7三个回归方程的截距项的解释力度分别在1%、10%、5%统计水平上显著。
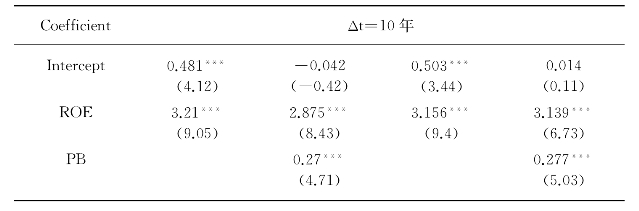
3.Δt=10年的加权平均回归结果
根据表4-4可以看出,当Δt=10年期时,ROE、PB的回归结果在1%水平上显著,但PE不显著。
表4-4 加权平均回归结果(Δt=10年)
续表

注:***、**、*分别表示在1%、5%和10%统计水平上显著。
同时可以看出,10年期的股票收益,来自ROE单一因素的解释力度为56.13%,ROE、PB两个因素共同作用,解释力度为70.62%,比单一ROE因素的解释力度增加14.49%。
但是,若ROE、PE两个因素共同作用,解释力度为61.76%,比单一ROE因素的解释力度仅增加5.63%,可见PE因素的影响小于PB因素的影响。
若ROE、PB、PE三个因素共同作用,则对股票收益来源的解释力度达到75.63%,比单一ROE因素的解释力度增加19.50%,比ROE、PB两个因素的解释力度仅增加5.01%,可见ROE、PB两个因素基本决定了10年期股票的收益,而且ROE是最核心的因素,解释力度超过50%。
而且,通过表4-4可以得到基于ROE、PB、PE三个因素依次进行回归的10年期回归方程。(https://www.xing528.com)

从截距项(intercept)来看,式4-9、式4-11两个回归方程的截距项的解释力度分别在1%统计水平上显著。
4.Δt=20年的加权平均回归结果
根据表4-5可以看出,当Δt=20年期时,ROE、PB的回归结果在1%水平上显著。ROE/PB/PE三因素回归方程中,PE为5%统计显著。
表4-5 加权平均回归结果(Δt=20年)

注:***、**、*分别表示在1%、5%和10%统计水平上显著。
同时可以看出,20年期的股票收益,来自ROE单一因素的解释力度为60.51%,ROE、PB两个因素共同作用,解释力度为72.88%,比单一ROE因素的解释力度增加12.37%。
但是,若ROE、PE两个因素共同作用,解释力度为64.05%,比单一ROE因素的解释力度仅增加3.54%,可见PE因素的影响小于PB因素的影响。
若ROE、PB、PE三个因素共同作用,则对股票收益来源的解释力度达到76.83%,比单一ROE因素的解释力度增加16.32%,比ROE、PB两个因素的解释力度仅增加3.95%,可见ROE、PB两个因素基本决定了20年期股票的收益,而且ROE是最核心的因素,解释力度超过60%。
通过表4-5可以得到基于ROE、PB、PE三个因素依次进行回归的20年期回归方程。
![]()

从截距项(intercept)来看,式4-13、式4-14、式4-15三个回归方程的截距项的解释力度分别在1%、5%、1%统计水平上显著。
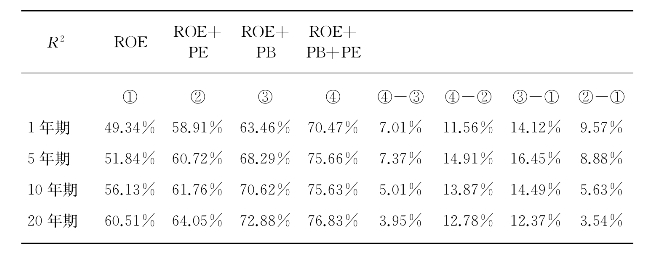
综上,对不同周期三个因素组合的解释力度整理如表4-6。
表4-6 不同周期三因素组合的解释力度(加权平均)
该表构建的图形见图4-14和图4-15。

图4-14 不同周期三因素组合的解释力度1(加权平均)

图4-15 不同周期三因素组合的解释力度2(加权平均)
结合表4-6与图4-14、图4-15可以看出:
(1)ROE、PB、PE三个因素组合对股票收益的解释力度区间为70.47%—76.83%,解释力度最好的是20年期,为76.83%。
(2)ROE、PB两因素组合对股票收益的解释力度区间为63.46%—72.88%,解释力度最好的是20年期,为72.88%。
(3)ROE单一因素对股票收益的解释力度为49.34%—60.51%,解释力度最好的是20年期,为60.51%。随着时间的推移,从1年期、5年期、10年期、20年期,ROE的解释力度在持续上升。
(4)无论是1年期、5年期、10年期还是20年期,ROE、PB、PE三因素组合相对于ROE、PE两因素组合,也就是不考虑PB因素,对股票收益的解释力度增加11.56%—14.91%(见表4-6④-②列);ROE、PB、PE三因素组合相对于ROE、PB两因素组合,也就是不考虑PE因素,对股票收益的解释力度只增加3.95%—7.01%(见表4-6④-③列),也就是说PB因素对股票收益影响大于PE因素。
(5)从回归结果来看,变量PB的回归系数更加显著,变量PE的回归系数则不显著。因此,在控制ROE情况下,PB对股票回报率有显著的影响,而PE的影响则并不显著。
以上五点,可以参见图4-16。
在投资组合采用加权平均法进行收益率检验,有效地支持了假设H5,对前文“3.3.2 变量回归结果检验”再次成功进行稳健性检验。
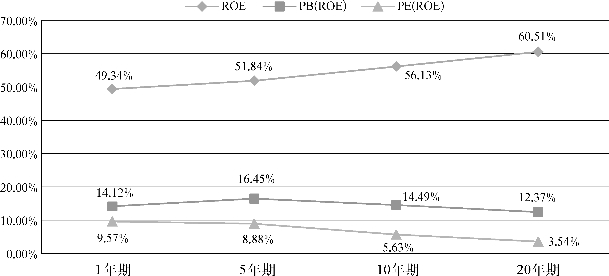
图4-16 三因素回归的加权平均收益
H5:长期来看,市场因素(PE、PB)对股票收益的影响较小,基本面ROE影响较大。
同时可以进一步得到以下结论。
长期来看,投资组合收益的影响因素中,基本面ROE影响最大,市场因素(PE、PB)的影响较小,而且PB因素的影响大于PE因素的影响。
ROE对投资组合收益的解释力度为50%—60%,PB对投资组合的收益解释力度为12%—16%左右,PE对投资组合的收益解释力度为3%—10%左右。
无论是短期(1年)还是长期(5—20年),ROE、PB、PE三个因素的共同对投资组合的解释力度超过了70%。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




