晨读经典：三角函数奇偶性

一、同角三角函数基本关系式

平方关系：sin2α＋cos2α＝1；　商数关系：．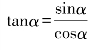

二、诱导公式（k∈Z）

公式一：sin（α＋2kπ）＝sinα，cos（α＋2kπ）＝cosα，tan（α＋2kπ）＝tanα．

公式二：sin（－α）＝－sinα，cos（－α）＝cosα，tan（－α）＝－tanα．

公式三：sin（π－α）＝sinα，cos（π－α）＝－cosα，tan（π－α）＝－tanα．

公式四：sin（π＋α）＝－sinα，cos（π＋α）＝－cosα，tan（π＋α）＝tanα．

公式五：sin（2π－α）＝－sinα，cos（2π－α）＝cosα，tan（2π－α）＝－tanα．

公式六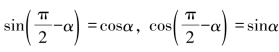：．(www.xing528.com)

记忆口诀：奇变偶不变，符号看象限。奇偶指的奇偶数倍，变与不变指三角函数名，若变，则是正弦变余弦，余弦变正弦。符号是根据角的范围以及三角函数在四个象限的正负来判断新三角函数的符号（无论α多大，都将α看成锐角）。

三、三角恒等变换

两角和与差的三角函数及二倍角的三角函数公式：

sin（α＋β）＝sinαcosβ＋cosαsinβ，sin（α－β）＝sinαcosβ－cosαsinβ．

cos（α＋β）＝cosαcosβ－sinαsinβ，cos（α－β）＝cosαcosβ＋sinαsinβ．

sin2α＝2sinαcosα，．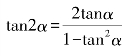

cos2α＝cos2α－sin2α＝2　cos2α－1＝1－2　sin2α．