决策现金持有量：实用案例与模型

企业持有现金过多，会使盈利水平下降，而现金太少，又可能出现现金短缺，影响生产经营。出于成本和收益关系的考虑，必须确定最佳现金持有量。当前应用较为广泛的现金持有量决策方法主要有成本分析模型、存货模型以及米勒－奥尔模型。

1.成本分析模型

成本分析模型是根据企业持有现金的机会成本、管理成本和短缺成本的分析来决定最佳现金持有量。

（1）机会成本

现金的机会成本是指企业因保留一定现金余额而丧失的再投资收益。这种投资收益是企业不能用该现金进行其他投资而丧失的收益，与现金持有量呈正相关关系，企业持有的现金越多，所需的机会成本越大。持有现金的机会成本可以用下式估计：

（2）管理成本

现金的管理成本是指企业因保留一定现金余额而增加的管理费用，如现金管理人员的工资。现金管理成本不随企业的现金持有量的多少而变动，是一种固定成本，与现金持有量不存在比例关系。

（3）短缺成本

现金的短缺成本是指企业因现金短缺而遭受的损失，是因现金持有量不足而又无法及时通过有价证券变现加以补充而给企业造成的损失。例如，不能按时支付购料款而影响与供货单位的关系，造成停工待料；因透支银行存款而影响企业与银行的关系，造成申请贷款困难等。企业持有现金的短缺成本随企业持有现金量的增加而下降，与现金持有量负相关。

最佳现金持有量是上述三项成本之和最小时的现金持有量。

2.存货模型

确定最佳现金持有量的存货模型源于存货的经济批量模型。这一模型最早由美国学者W.J.Baumol于1952年提出，因此又称为鲍摩尔（Baumol）模型。

在存货模式中，假设收入是每隔一段时间发生一次，而支出则是在一定时期内均匀发生的。在此期间，企业可通过销售有价证券获得现金，如图8－7所示。

图8－7　确定现金余额的存货模型

在图8－7中，假设企业0时点持有现金N 元，由于现金流入的速度小于现金流出的速度，在T1时点企业的现金余额下降为0，此时企业通过出售N 元的有价证券补充现金。随后，当现金余额在T2时点再次下降为0时，企业再次出售价值N 元的有价证券，循环往复。

存货模式的目的是求出使总成本最小的现金持有量。现金持有的总成本包括现金持有成本和现金转换成本两个方面。

（1）现金持有成本，即持有现金所放弃的报酬，是持有现金的机会成本，这种成本通常为有价证券的利息率，它与现金持有量成正比例变化。

（2）现金转换成本，即现金与有价证券相互转换的固定成本，可以理解为交易成本。例如，经纪人佣金、捐税及其他管理成本，这种成本只与交易的次数有关，而与每次转换现金的数额无关。

如果持有现金量大，则持有现金的机会成本高，但转换成本下降；如果持有现金量小，则持有现金的机会成本低，但转换成本上升。两种成本总和最低时的现金量即为最佳现金持有量。

一定时期内，持有现金的总成本为：

式中，TC为总成本；b为现金与有价证券的转换成本；T为特定时间内的现金总额；N为理想的现金转换数量（最佳现金持有量）；i为短期有价证券利息率。

上式是一个以N为自变量、以TC为因变量的函数。对该函数求极值，可以采用求一阶导数的方法求出令总成本TC 最小时的N 值，如下所示

令TC′＝0，则有i／2＝T·b／N2，可得。

所以最佳现金持有量的计算公式为：(www.xing528.com)

当企业以最佳现金持有量水平持有现金时，其一定时期内的总成本为：

存货模型可以精确地测算出最佳现金持有量和变现次数，表述了现金管理中基本的成本结构，它对加强企业的现金管理有一定作用。但是这种模型以货币支出均匀发生、现金持有成本与转换成本易于预测为前提条件。因此，只有在上述因素比较确定的情况下才能使用此模型。

【例8－1】　樱兰公司预计全年需要现金300 000元，现金与有价证券的转换成本为每次200元，有价证券的年利息率为7.5%。樱兰公司的最佳现金余额为多少？

解　

当公司按照这一最佳数额持有现金，那么公司每年从有价证券转换为现金的次数为：

300 000÷40 000＝7.5（次）

全年总成本为：

其中，公司全年承担的机会成本为：（40 000÷2）×7.5%＝1 500（元）；公司全年承担的转换成本为：7.5×200＝1 500（元）。两者总计为3 000元，这一结果与上述计算结果一致。

3.米勒－奥尔模型

米勒－奥尔（Miller－Orr）模型由默顿·米勒（Merton Miller）和丹尼尔·奥尔（Daniel Orr）创建，是一种基于不确定性的现金管理模型。该模型假设企业无法确切地预知每日实际收支状况，现金流量服从正态分布，现金与有价证券之间能够自由兑换。

在米勒－奥尔模型中，既引入了现金流入量也引入了现金流出量。模型假设日现金净流量（现金流入量减去现金流出量）服从正态分布，每日的现金净流量可以等于其期望值，也可以高于或低于其期望值。图8－8对现金余额的随机波动情况进行了描述。

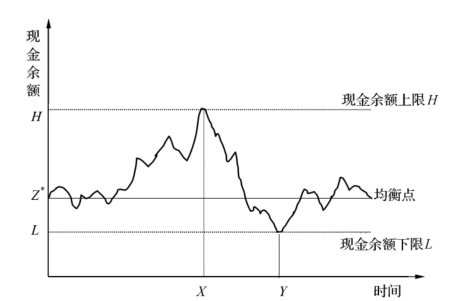
图8－8　确定最佳现金余额的米勒－奥尔模型

图8－8说明了米勒－奥尔模型的基本原理。该模型是建立在对控制上限（H）、控制下限（L）以及目标现金余额（Z＊）这三者进行分析的基础之上的。企业的现金余额在上、下限间随机波动，在现金余额处于H和L 之间时，不会发生现金交易。当现金余额升至H 时，比如说点X（上限），则企业购入H－Z＊单位（元）的有价证券，使现金余额降至Z＊。同样地，当现金余额降至L，如点Y（下限），企业就需售出Z＊－L 单位（元）的有价证券，使现金余额回升至Z＊。这两种情况都是使现金余额回到Z＊。

与鲍摩尔模型相同的是，米勒－奥尔模型也依赖于交易成本和机会成本，且每次转换有价证券的交易成本被认为是固定的，而每期持有现金的百分比机会成本则是有价证券的日收益率。与鲍摩尔模型不同的是，米勒－奥尔模型每期的交易次数是一个随机变量，且根据每期现金流入与流出量的不同而发生变化。根据米勒－奥尔模型，最佳现金余额Z＊的计算公式为：

式中，L 代表现金余额下限；σ 代表每日现金余额变化的标准差；b 代表现金与证券的固定转换（交易）成本；r 代表有价证券的日收益率。

L 的设置受到企业日常周转所需最低现金量、企业的借款能力、管理人员对现金短缺风险的愿意承受程度等因素的影响，最低可确定为零。

现金余额上限的计算公式为：

【例8－2】　樱兰公司目前的证券交易成本为每次500元，有价证券的日均收益率为0.06%。根据公司管理人员承受风险的倾向以及每日现金最低需求量，财务部确定的每日最低现金需要量为200元。根据最近4年的现金余额情况，测算出日现金余额标准差为5 000元。樱兰公司的最佳现金持有量和持有量上限分别为多少？

解　最佳持有量为：

持有量上限为：