1.证券投资组合的风险分散效应
投资组合理论认为,若干种证券组成的投资组合,其收益是这些证券收益的加权平均数,但是其风险不是这些证券风险的加权平均风险,投资组合能降低风险。
这里的“证券”是“资产”的代名词,它可以是任何产生现金流的东西,例如一项生产性实物资产、一条生产线或者一个企业。
【例6-6】 假设投资100万元,A和B各占50%。如果A和B完全负相关,即一个变量的增加值永远等于另一个变量的减少值,组合的风险被全部抵消,如表6-1所示。如果A和B完全正相关,即一个变量的增加值永远等于另一个变量的增加值,组合的风险不减少也不扩大,如表6-2所示。
表6-1 完全负相关的证券投资组合数据

表6-2 完全正相关的证券投资组合数据
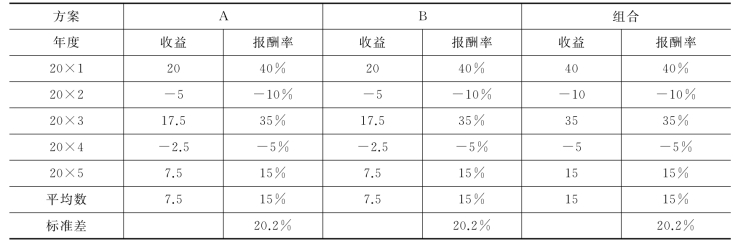
各种证券之间通常不太可能完全正相关或完全负相关,所以证券投资组合可以降低风险,但又不能完全消除风险。一般而言,证券的种类越多,风险分散效应越大,证券投资组合的风险越小。
以上我们看到的是两种证券不同组合时的风险分散效应,如果将市场上的所有证券(或资产)纳入到投资组合中来,其风险分散效应如图6-1所示。
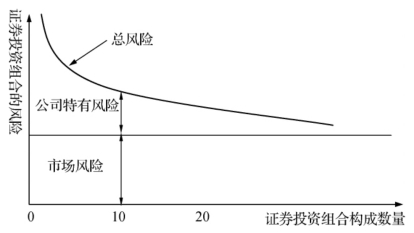
图6-1 证券投资组合的风险
承担风险会从市场上得到回报,回报大小仅仅取决于系统风险。这就是说,一项资产的期望报酬率高低取决于该资产的市场风险大小。
2.证券投资组合的风险与β系数
(1)非系统风险。非系统风险又叫作可分散风险或者公司特别风险,是某一因素或事件只会对特定的证券带来价格波动或者对某一投资者带来收益不确定影响的可能性。投资者对非系统风险应尽可能消除。
(2)系统风险。系统风险又叫作不可分散风险或者市场风险,是某一种因素对市场上所有证券都会带来价格波动或者对所有投资者带来收益不确定影响的可能性。投资者对系统风险无法消除,但可回避。单项资产或资产组合受系统风险影响的程度可以通过β系数来衡量。
β系数又可称为系统风险系数,是美国经济学家威廉·夏普提出的风险衡量指标。β系数是个相对指标,反映证券组合被动性与市场波动性的比例,揭示单项资产(或证券组合,下同)收益率与市场平均收益率之间的变动关系。在一般情况下,将某个具有一定权威性的股指作为测量股票β系数的基准,也称为市场组合。如果基准为1.0,而β系数为1.1,即表明该股票的波动性要比市场大盘高10%;同理,如β系数为0.95,则说明该股票的波动性弱于市场大盘。β系数可较方便准确地反映投资收益与风险之间的关系。系统风险系数的计算公式如下:

式中,ρi,m为第i项资产收益率与市场组合收益率的相关系数;σi为第i项资产收益率的标准差,表示该资产的风险大小;σm为市场组合收益率的标准差,表示市场组合的风险大小;COV(Ri,Rm)为第i项资产收益率与市场组合收益率的协方差,等于三个指标的乘积ρi,mσiσm。
证券投资组合的β系数是该证券投资组合中各单项资产β系数的加权平均数,如下所示

式中,Wi为证券投资组合中每一单项资产占证券投资组合总价值的百分比:

β系数越大的资产,其预期收益率也越大;否则,该资产就会增加证券投资组合的风险,却不能同比增长预期收益率,这样的市场证券组合也就算不上是最佳的市场风险投资组合。所以只要从中剔除这种不起积极作用的证券,就可使该组合的预期收益率相对于它的风险度而增加。因此可以说β系数与预期收益率是一种正相关关系,也可以说,无风险证券的β系数等于零。证券投资组合相对于自身的β系数就是1。
证券与证券投资组合的β系数衡量的是相对于某一特定证券投资组合——市场证券组合,证券与证券组投资合收益的波动性。个别公司因经营亏损发生股价剧烈波动的情况不应在β系数的衡量范围内。β值衡量的风险属于系统风险,即无法通过投资分散化予以消除,而非系统风险是由单个证券的收益波动来决定的,可通过投资分散化来消除。人们只需知道某种证券过去一系列的收益数据以及作为参照物的特定证券投资组合,即市场证券组合在相应年份的变动数据,就可得出该证券的β系数,而证券投资组合的β系数就是该组合中各证券β系数的加权平均数。β>1,表示该项投资风险大于整个市均风险;β<1,表示该项投资风险小于整个市均风险;β=1,表示该项投资风险等于整个市均风险。
【例6-7】 某投资人持有共100万元的3种股票,其中A 股票30万元、B 股票30万元、C股票40万元,β系数均为1.5,则综合β系数为:
β(ABC)=30%×1.5+30%×1.5+40%×1.5=1.5
若他将其中的C股票出售并买进同样金额的D 股票,D 的β系数为0.1,则:
β(ABD)=30%×1.5+30%×1.5+40%×0.1=0.94(https://www.xing528.com)
可见,构成组合的单个证券的β系数减小,则组合的综合β系数降低,使组合的风险减小;反之,则风险增大。投资者可以据此选择自己能接受的风险水平。但是,降低风险的同时,收益率也会降低。
3.证券投资组合的预期收益率
假如有两种股票,每种股票的预期收益率都是10%,且持股比例相等,均为50%,则由这两种股票构成的投资组合的预期收益率也肯定等于10%。这一结果意味着你不会因为投资某种股票数量的多少而减少投资组合的预期收益率,即投资组合的预期收益率是构成组合的各个证券的预期收益率的简单加权平均数,如下所示:

式中,Ri为单个证券的预期收益率;Wi为单个证券在投资组合中投资价值的比重;n为投资组合中证券的种类。
假设A、B、C、D 四种证券的预期收益率分别为R1=18%、R2=15%、R3=20%、R4=13%,投资组合中各证券的比重见例6-7,则两种投资组合的预期收益率分别为:
R(ABC)=18%×30%+15%×30%+20%×40%=17.9%
R(ABD)=18%×30%+15%×30%+13%×40%=15.1%
如果该组合的预期收益率高于投资者要求的收益率,则该组合可行,否则应进行调整。
投资者可以优先选择低风险方案,如ABD 组合,但只能得到15.1%的预期收益率;投资者也可以优先选择高预期收益率方案,如ABC组合,可以得到17.9%的预期收益率,但必须承担较高的风险。投资者确定了风险水平后,可通过选择证券种类,优化证券投资组合,在不提高风险的条件下使预期收益率最高。或者在确定预期收益率之后,优化证券投资组合,使风险降至最低。
4.证券组合风险的测定
风险是指投资者投资于某种证券的不确定性,即指遭受损失的可能性。实际发生的收益率与预期收益率的偏差越大,投资于该证券的风险也就越大。
(1)双证券投资组合风险的测定
双证券投资组合的风险不能简单地等于单个证券的风险以投资比重为权数的加权平均数,因为两种证券的风险具有相互抵消的可能性。这就需要引进协方差和相关系数的概念。
①协方差。协方差是表示两个随机变量之间关系的变量,它是用来确定证券组合收益率方差的一个关键性指标。若以A、B两种证券的投资组合为例,则其协方差为:
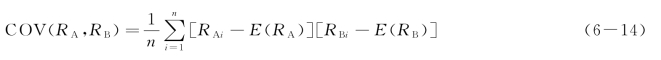
式中,RA为证券A 的收益率;RB为证券B的收益率;E(RA)为证券A 的收益率的期望值;E(RB)为证券B的收益率的期望值;n为证券种类数;COV(RA,RB)为A、B 两种证券收益率的协方差。
②相关系数。相关系数也是表示两种证券的收益变动的相互关系的指标。它是协方差的标准化,其公式为:

其中,COV(RA,RB)=ρABσAσB。相关系数ρAB的取值范围介于-1与+1之间:当取值为-1时,表示证券A和B的收益变动完全负相关;当取值为+1时,表示证券A和B的收益变动完全正相关;当取值为0时,表示证券A和B 的收益变动完全不相关;当0<ρAB<1时,表示证券A和B的收益正相关;当-1<ρAB<0时,表示证券A和B的收益负相关。
③双证券投资组合的标准差。计算公式如下所示:
![]()
因此,影响证券投资组合风险的因素主要是组合中每种证券所占的比例、证券收益率的相关性和每种证券的标准差。
(3)多证券投资组合风险的测定
多证券投资组合风险测定的基本原理同双证券投资组合的一样,可用如下公式来表示:

式中,WiWj为第i种、第j 种证券在证券投资组合中所占的比重;covij为第i 种证券和第j种证券的协方差;ρij为第i种证券和第j 种证券的相关系数。
随着投资组合中证券数目的增加,在决定组合方差时,协方差的作用越来越大,而方差的作用越来越小,这一点可以通过考察方差-协方差矩阵得知。在一个由两种证券组成的投资组合中,有两个加权方差和两个加权协方差;随着组合中证券数目的增加,任意两种证券间的协方差在式(6-17)中出现的个数将快速增加,其对总方差的影响越来越大于各证券方差对总方差的影响,因此,对于一个大的投资组合,总方差主要取决于任意两种证券间的协方差,若一个投资组合进一步扩大到包括所有的证券,则协方差几乎就成了投资组合标准差的决定性因素。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




