航空材料力学性能检测数据处理成果

1.弯曲强度的计算

选用三点弯曲加载方式时，按式（10-13）计算弯曲强度σ_f。即

σ_f=3P_maxl/（2bh²） （10-13）

式中 P_max——最大载荷（N）；

l——跨距（mm）；

b——试样宽度（mm）；

h——试样厚度（mm）。

P值的选取方法如下：

1）ASTM D7264—2015规定：试验记录的最大载荷。

2）ASTM D790—2015e2规定：试验记录的最大载荷。

3）GB/T 1449—2005规定：挠度在小于或等于1.5倍试样厚度下破坏的材料，取破坏时最大载荷；挠度超过1.5倍试样厚度不呈现破坏的材料，取挠度为1.5倍试样厚度对应的载荷。

4）GB/T 3356—2014规定：试样破坏时的最大载荷。

2.弯曲应变的计算

选用三点弯曲加载方式时，按式（10-14）计算试样下表面的弯曲应变ε_f。即

ε_f=6δh/l² （10-14）

式中 δ——试样下表面中心的挠度（mm）；

l——跨距（mm）；

h——试样厚度（mm）。

3.弯曲模量的计算

（1）GB/T 3356—2014中弯曲弹性模量的计算 按GB/T 3356—2014的规定，其弯曲弹性模量E_f按式（10-15）计算。即

式中 ΔP——载荷-挠度曲线上初始直线段的载荷增量（N）；

Δδ——对应于ΔP的试样跨距中点处的挠度增量（mm）；

l——跨距（mm）；

h——试样厚度（mm）；

b——试样宽度（mm）。

（2）GB/T 1449—2005中弯曲弹性模量的计算 按GB/T 1449—2005的规定，对于给定的应变ε₁=0.0025、ε₂=0.0005下，其弯曲弹性模量E_f按式（10-16）计算。即

E_f=500（σ₁-σ₂） （10-16）(www.xing528.com)

式中 σ₁——应变ε₁=0.0025时测得的弯曲应力（MPa）；

σ₂——应变ε₂=0.0005时测得的弯曲应力（MPa）。

（3）ASTM D7264—2015中弯曲弹性模量的计算 按ASTM D7264—2015的规定，对于给定的应变ε₁=0.001、ε₂=0.003下，其弯曲弹性模量E_f按式（10-17）计算。即

式中 σ₁——应变ε₁=0.001时测得的弯曲应力（MPa）；

σ₂——应变ε₂=0.003时测得的弯曲应力（MPa）。

（4）ASTM D790—2015e2中弯曲弹性模量的计算 按ASTM D790—2015e2的规定，弯曲弹性模量E_f按式（10-18）计算。即

E_f=（σ₂-σ₁）/（ε₂-ε₁） （10-18）

式中 ε₁、ε₂——应力-应变曲线线性段上预先定义的两点处的应变（mm/mm）；

σ₁、σ₂——与ε₁、ε₂分别对应的弯曲应力（MPa）。

4.大跨距梁的修正

ASTM D790—2015e2规定：当采用较大的跨厚比时，在支辊处会产生明显的应力集中，从而对简支梁的弯曲产生影响。大跨厚比的梁会出现相对较大的位移。如果跨厚比大于16，加载位移超过跨距的10%时，可以采用式（10-19）近似计算简支梁试件外表面的弯曲应力值。即

σ_f=（3Pl/2bh²）[1+6（δ/l）²-4（h/l）（δ/l）] （10-19）

式中 P——载荷-位移曲线上给定点的载荷（N）；

δ——试样下表面中心的挠度（mm）；

l——跨距（mm）；

b——试样宽度（mm）；

h——试样厚度（mm）。

5.底部补偿

1）典型的应力-应变曲线（图10-11）含有一个底部区域AC，它并不代表材料的特性，而是由于试验系统间隙的拉紧和试件的对中度或安装定位等人为因素造成的。为了获得正确的参数值，如弹性模量、应变、偏移屈服点，必须对这些人为因素进行补偿，以给出修正的应变零点或延长轴线。

2）对于具有明显线性行为的材料（图10-11），曲线线性段（CD）的延长线应该通过应力轴线的零点。截距点（B）即为应变零点，如果可能，必须测量所有的延长值或应变值，包括屈服偏移量（BE）。直线CD（或其延长线）上任意一点的应力值除以同一点的应变值（从应变零点B测量）即可得到弹性模量。

3）对于不具有任何线性区的材料（图10-12），在拐点H′处沿最大斜率构造一条切线，可以得到同样的应变零点底部修正。延长线与应变轴向相交于点B′，即修正的应变零点。将点B′作为应变零点，曲线上任意一点（G′）的应力值除以该点的应变值即可得到切线模量（直线B′G′的斜率）。对于没有线性区的材料，不建议使用通过拐点的切线作为基准来确定偏移屈服点。

对于任何一种复合材料体系，弯曲性能已经成为必不可少的性能评价参数之一，但由于复合材料弯曲试验中试样的应力状态复杂，弯曲性能的影响因素较多，可能发生多种失效模式。不同试验方法对弯曲试验有效性的规定不一，因而对复合材料弯曲性能数据的统计分析及对材料性能的评价，应根据具体情况谨慎对待。

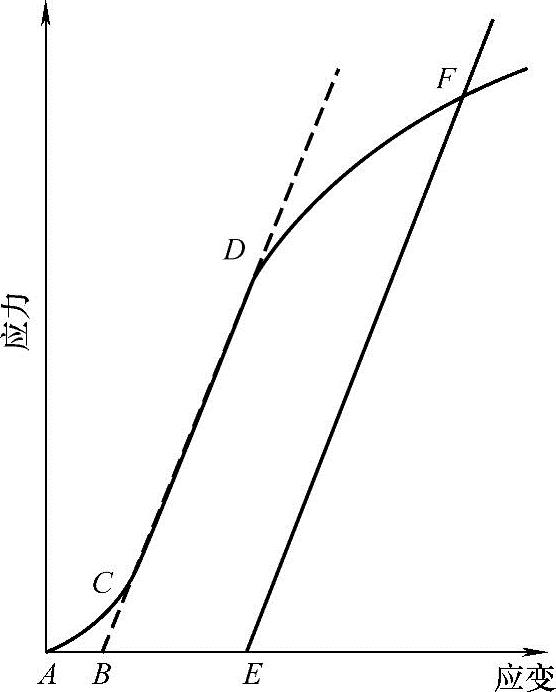
图10-11 具有线性区域的材料

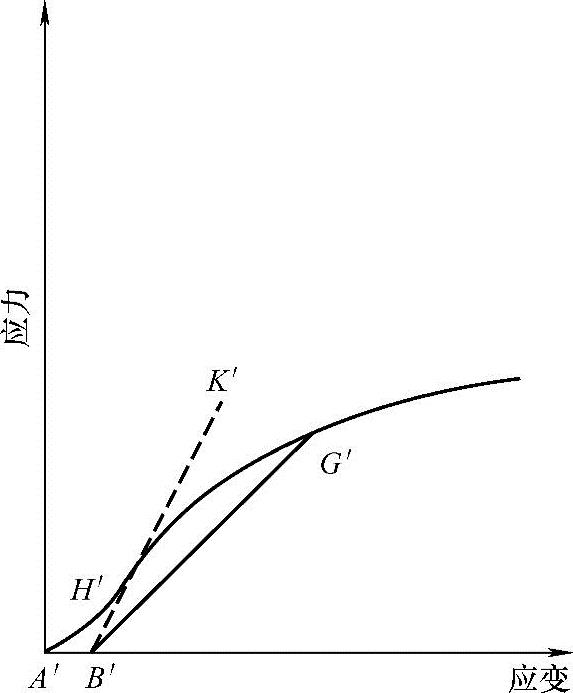
图10-12 没有线性区域的材料