航空材料弹塑性状态下的断裂韧度检测

线弹性断裂力学原理和方法在研究和解决脆性断裂方面取得了巨大的成效。然而对于塑性较好的延性材料，裂纹尖端的塑性区尺寸往往较大，以至于超过了“小范围屈服”的条件，此时线弹性断裂力学的理论基础和断裂判据K_Ⅰ=K_Ⅰc已经失效，必须重新建立新的判据，此时需要采用弹塑性断裂力学的理论来解决。由于弹塑性断裂力学处理裂纹体问题比较复杂，目前这部分理论基础和试验方法尚处于发展阶段，远不如线弹性断裂力学完善，但由于它研究的问题更接近于实际，因此发展很快。目前应用最广的是裂纹尖端张开位移（CTOD）理论与J积分理论，下面分别介绍。

1.裂纹尖端张开位移（CTOD）理论

裂纹尖端张开位移的英文是Crack Tip Opening Displacement，可简写为CTOD或δ。CTOD理论主要有两种：一种是模型理论，另一种是经验理论。下面就模型理论的主要结论简介如下：

CTOD的模型理论为了计算大范围屈服条件下的裂纹尖端张开位移，从宏观模型和微观（位错）模型出发，得到的表达式如下

式中 σ_s——材料的屈服强度。

裂纹尖端的张开位移δ和应力σ、裂纹长度a有对应关系。用δ就可以描述大范围屈服条件下裂纹尖端的应力-应变场。式（13-29）一般称为D-M模型（宏观推导所得），也可称为BCS模型（从位错角度出发）。

在裂纹开始扩展的临界条件下

这就是D-M模型所给出的CTOD表达式，若将式（13-30）进行级数展开，并只取第一项，则可得

式（13-31）为D-M模型导出的δ、K_Ⅰ、G_Ⅰ的关系式。K_Ⅰ、G_Ⅰ在临界条件下的K_Ⅰc、G_Ⅰc是材料性能，所以δ_c也是材料性能。δ_c为那些测量K_Ⅰc有困难的中、低强度钢提供了依据。

2.J积分的定义

1968年，赖斯（J.R.Rice）提出了一个与积分路径无关的能量线积分，即J积分，其目的是用来分析缺口或裂纹所引起的应力集中问题。1972年，有人用试验测定了Ni-Cr-Mo-V转子钢和A533B压力容器用钢的断裂韧度J_Ⅰc，从而提出了J_Ⅰ=J_Ⅰc可以作为裂纹体弹塑性变形下的断裂准则，用该判据可以预测大范围屈服下裂纹尖端的开裂。下面就对J积分的定义、积分的性质以及J积分的计算做简要的介绍。(www.xing528.com)

（1）J积分的定义 弹塑性断裂力学的任务之一就是要提炼一个既能定量描述裂纹尖端应力-应变场的强度，又便于理论计算和试验测定的参量。赖斯从能量守恒出发提出一个严密的，围绕裂纹前缘从裂纹的一侧表面到另一侧表面的能量线积分的数学表达式，用以表征裂纹前缘区域的应力-应变场。

此定义的物理意义是：第一项是裂纹体的总应变能（包括了弹性应变能和塑性应变能），第二项是表示张力势能（内力势能），两项之差（即总应变能与势能之差）就表示这个弹塑性体的总位能。对不同材料制成的试样，J值的大小反映了裂纹尖端所受外界作用的强弱，所以J积分就是弹塑性情况下裂纹尖端应力场强弱程度的描述参量。

（2）J积分的特点 J积分有许多特点，其中较重要的如下：

1）J积分的数值与积分路径无关，即J积分路径的选取是任意的。这一特性称为J积分守恒性。

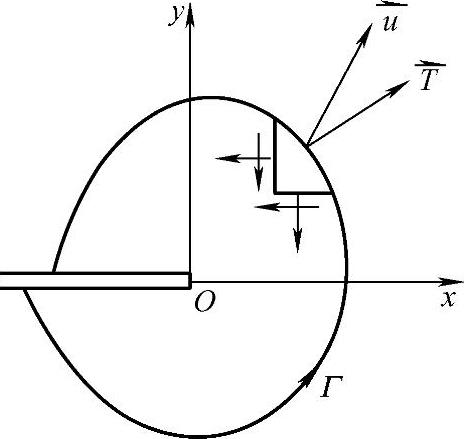
图13-10 J积分的定义

2）J积分可以描述在弹塑性状态下，裂纹前端应力-应变场的奇异性，它相当于线弹性状态下K_Ⅰ的作用。

（3）临界J积分（J_Ⅰc） 由式（13-32）可以推导得到，J积分就等于能量释放率G_Ⅰ，即

由于K_Ⅰ≥K_Ⅰc，G_Ⅰ≥G_Ⅰc是线弹性状态下的断裂判据，根据推理，J≥J_Ⅰc也是断裂判据。但是在弹塑性状态下利用J≥J_Ⅰc作为断裂判据是否合理，还只能用试验来证明。

应当指出，由于塑性变形不可逆，不允许卸载，而裂纹扩展就意味着部分卸载，故J积分原则上不能处理裂纹扩展问题。临界值J_Ⅰc指的是裂纹开始扩展的开裂点，而不是裂纹失稳扩展点。由于在线弹性状态下，J=G_Ⅰ，故J积分的量纲与G完全相同。