航空材料力学性能检测：应变-寿命曲线

材料的应变-寿命关系特性一般是低周疲劳试验关注的重点，是反映材料低周疲劳抗力最直接的依据。对于多根低周试样，不同的总应变范围Δε_t与其对应的断裂循环周次N_f之间建立起来的关系曲线称为应变-寿命（Δε_t-N_f）曲线，如图12-6所示。

疲劳寿命通常以循环次数的形式给出。考虑一个循环中在加卸载方向存在两次损伤，所以通常采用反向次数2N_f和应变幅Δε/2之间的关系来表征低周疲劳临界破坏行为。

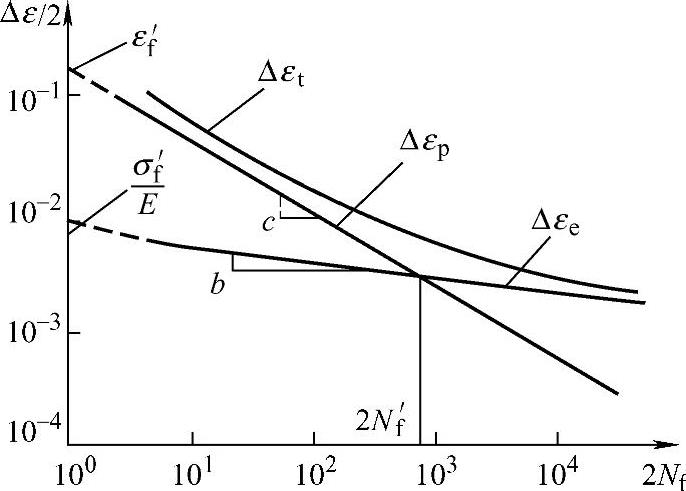
图12-6 应变-寿命曲线

材料在低周疲劳试验中，试样的失效寿命N_f可以基于不同的规定来确定，N_f可以取为试样断裂时对应的循环次数，也可以取为由稳定载荷幅下降到一定的百分比（比如5%或10%）对应的循环次数，有时也可以规定为出现特定尺寸的宏观裂纹长度所对应的循环次数。所以，在对比不同材料的疲劳寿命特性时应注意寿命规定的一致性。

低周疲劳的应变-寿命曲线，即总应变幅Δε_t/2和循环失效的反向次数2N_f之间的关系曲线。经验表明，Δε_t/2的弹塑性分量和2N_f的对数值之间符合线性关系，故低周疲劳应变-寿命曲线通常在双对数坐标上表示。Δε_t/2的弹性分量Δε_e/2与2N_f的关系可采用幂函数表示。即

式中 σ_f′——2N_f=1时直线的截距，称为疲劳强度系数。由于2N_f=1时相当于一次加载，所以可以粗略地取σ′_f=σ_f（静拉伸的真实断裂应力）；

b——斜率，称为疲劳强度指数。

Δε_t/2的塑性分量ε_p/2与2N_f的关系也可采用幂函数表示，又称为Manson-Coffin方程。即(www.xing528.com)

ε_p/2=ε_f′（2N_f）^c （12-5）

式中 ε_f′——2N_f=1时直线的截距，称为疲劳延性系数。同理，也可取ε_f′=ε_f（静拉伸的真实断裂应变）；

c——斜率，称为疲劳延性指数。

因此，Δε_t/2与2N_f的关系为

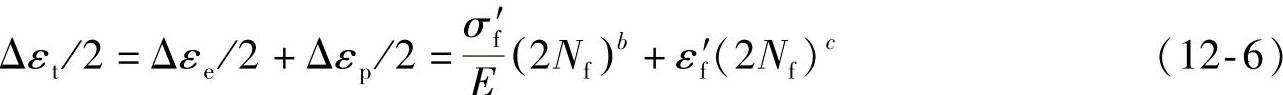
Δε_e/2-2N_f和Δε_p/2-2N_f曲线的交点所给出的寿命值称为过渡寿命N_t。此时，Δε_e=Δε_p，可以认为，在过渡寿命上，弹性应变所造成的损伤与塑性应变造成的损伤相等。当2N_f＞N_t时，Δε_e＞Δε_p，材料的疲劳寿命主要取决于Δε_e；当2N_f＜N_t时，Δε_p＞Δε_e，材料的疲劳寿命主要取决于Δε_p。由此可见，N_t相当于由以弹性应变损伤为主转向以塑性应变损伤为主的过渡寿命。

过渡寿命N_t是材料疲劳的关键指标之一。如果设计零部件的疲劳寿命2N_f＜N_t，则疲劳设计需要材料的低周疲劳数据和零部件受载的弹塑性解，如果2N_f比N_t大得多，则疲劳设计只考虑材料的高周疲劳数据和零部件的弹性解就可以了。

上述的σ_f′、b、ε_f′、c、k′、n′统称为应变疲劳参量，这些参量是综合评定材料疲劳性能的指标，σ_f′、b两个参量反映材料的应力疲劳性能，若σ_f′高、|b|低，则材料具有高的循环应力阻力。ε_f′、c两个参量反映材料的应变疲劳性能，若ε_f′高、|c|低，则材料具有高的循环应变阻力。