科技与金融搜寻匹配及政策效果研究：均衡增长路径

此部分考虑稳态的情况。根据劳动力市场的出清条件，均衡增长路径上，有：

将创新函数除以A得：

取对数并求导，可得：

由此可知，经济体中技术的进步率等于人口增长率。给定总生产函数的表达式，人均收入增长率y（=Y/L），一定也等于人口增长率n。

由公式（25），可知，能够确定稳态下r的价值（常数）为：

从公式（5），可以得到稳态下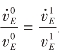。进一步地，由公式（6），可以得到：

稳态下，等式左侧为常数，则有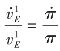。从公式（19）可知后者等于n，则有：

由条件（29），可得和的表达式如下：(www.xing528.com)

重复同样的步骤，可得和的表达式如下：

定义就业率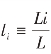,i=Y,E,F，得到以下稳态均衡方程组：

其中和ω的表达式分别由式（32）—（33）、式（34）—（35）和式（16）给出。

前两个方程表明，稳态均衡条件下，劳动者选择成为资本家还是企业家，或者是普通生产工人，获得的报酬率是相同的。需要注意的是，ω是确定的收入，而和则是期望值。Grossman和Helpman（1991）指出，即使对于风险厌恶型劳动者，该稳态均衡也是成立的。理由在于，在创新驱动增长模型中，劳动者能够通过金融中介，无成本地将其投资组合完全分散于不同的中间产品部门，因此能够完全规避创新收益的波动性。第三个方程表示劳动市场的出清条件。前两个等式能够被解释为资本家和企业家之间隐含的最优反应函数，很容易证实这些函数都是正斜率，即dli/dl-i＞0（i=E，F），意味着在创新过程中的两个主要参与方之间存在战略互补。第一个方程捕捉的是资本家对企业家的影响，lF增加提升了与企业家的匹配概率αE，增加了企业家的预期收益，引致企业家数量的增加。同理可分析第二个方程。

使用式（32）—（33）、式（34）—（35）、式（16）和式（19），以及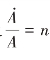，αE=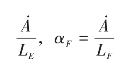，可将方程组（36）写为：

其中，。由于无法通过方程组（37）解出lE、lF和lY的具体值，因此企业家和资本家之间的战略互补预示着理论上存在多重均衡的可能性。

在创新驱动增长模型中，新的中间产品带来的垄断收益π将在资本家和企业家之间进行分配，接下来将分别通过市场化的收益分配和基于纳什议价的收益分配两种方法讨论具体分配比例的确定。