时间序列ARMA模型

时间序列分析方法是伯克斯（Box）和詹金斯（Jenkins）1976年提出的。目前，这种方法已广泛应用于自然科学和社会科学的各个领域。这种分析方法不考虑其他解释变量的作用，而是依据变量本身的变化规律，利用外推机制描述时间序列的变化，是一种定量预测方法。

首先介绍与时间序列相关的几个定义。

由随机变量随时间组成的有序序列称为随机过程，可记为｛xt｝或xt。

随机过程的一次观测结果称为时间序列，时间序列中的元素称为观测值。

对于一个随机过程｛x，t∈T｝，如果∀t∈T；Cov（xt，xt＋k）＝0，　（t＋k）∈T，k≠0，则称｛xt｝为白噪声过程。白噪声是平稳的随机过程，其均值为零，方差为固定值。随机变量之间非相关。

时间序列模型有三种基本类型：自回归模型（Autoregressive Model，简称AR模型）、移动平均模型（Moving Average Model，简称MA模型）以及自回归移动平均模型（Autoregressive Moving Average Model，简称ARMA模型）。

（1）自回归模型（AR模型）。

如果一个线性随机过程可表达为：

其中，Øi，i＝1，…，p是回归参数，ut是白噪声过程，则这个线性过程xt称为p阶自回归过程，用AR（p）表示。它是由xt的p个滞后变量的加权以及ut相加而成的。记LP为p步滞后算子，即Lpxt＝xi-p，则模型可表示为：

其中，Φ（L）＝1-Ø1L-Ø2L2-…-ØpLp称为自回归算子或自回归特征多项式。

与自回归模型常联系在一起的是平稳性问题。对于自回归过程AR（p），如果特征方程Φ（L）＝0的所有根的绝对值都大于1，则该过程是一个平稳过程。对于一般的自回归过程AR（p），特征多项式可以分解为

其中，是特征方程Φ（L）＝0的根，由式（7.2），xt可表达为：

其中，k1，k2，…，kp是待定常数。xt具有平稳性的条件是Φ（L）-1必须收敛，即应有p是特征方程Φ（L）＝0的根，所以保证AR（p）过程具有平稳性的条件是特征方程的全部根必须在单位圆（半径为1）之外，即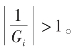

（2）移动平均模型（MA模型）。(www.xing528.com)

如果一个线性随机过程可用下式表达：

其中，θ1，θ2，…，θq是回归参数，ut为白噪声过程，则称式（7.5）为q阶移动平均过程，记为MA（q）。因为xt是由ut和ut的q个滞后项的加权和构造而成，所以称其为移动平均过程。“移动”只随着时间t变化，“平均”指加权和之意。上式还可以用滞后算子写为：

或

其中，Θ（L）＝（1＋θ1L＋θ2L2＋…＋θqLq），称为移动平均算子或移动平均特征多项式。由定义知任何一个q阶移动平均方程都是由（q＋1）个白噪声变量的加权和组成的，所以任何一个有限阶移动平均过程都是平稳的过程。

与移动平均过程相联系的一个重要概念是可逆性。移动平均过程具有可逆性的条件是特征方程全部根的绝对值必须都大于1，特征方程表示为：

由式（7.7），xt＝Θ（L）ut有Θ（L）-1xt＝ut。由于Θ（L）可表示为：

所以

可见，保证MA（q）过程可以转换成一个无限阶自回归过程，即MA（q）具有可逆性的条件是Θ（L）收敛。即必须有2，…，q成立。而是特征方程Θ（L）＝0的根，所以MA（q）过程具有可逆性的条件是特征方程Θ（L）＝0的根必须在单位圆之外。

（3）自回归移动平均模型（ARMA模型）。

由自回归和移动平均两部分共同构造的随机过程称为自回归移动平均过程，记为ARMA（p，q），其中p，q分别表示自回归和移动平均分量的最大滞后阶数。ARMA（p，q）的一般表达式是：

或

其中Φ（L）和Θ（L）分别表示关于L的p，q阶特征多项式，分别称为自回归算子和移动平均算子。

ARMA（p，q）过程的平稳性只依赖于其自回归部分，即Φ（L）＝0的全部根取值在单位圆之外（绝对值大于1）。其可逆性则只依赖于移动平均部分，即Θ（L）＝0的根取值应在单位圆之外。