技术创新、资本投入、人才流动对区域经济增长的统计和经济解释

本书模型中的有关参数均采用最小二乘（OLS）回归的方法，运用Stata15.0软件估计得出。为了更好地理解技术创新、资本投入、劳动力投入、人才流动对区域经济增长的贡献率，有必要对参数给予统计意义上和经济意义上的解释。假设被解释变量Y是解释变量X1，X2，…，Xk和随机误差项u的线性函数，它们可以表示为如下公式：

称为多元总体线性回归模型。

设（X1i，X2i，…，Xki；Yi），i＝1，2，…，n是对总体（X1，X2，…，Xk；Y）的n次独立样本观测值，将它们代入式（6.10），得到以下公式：

式（6.10）是样本数据结构形式的多元总体线性回归模型，它是由n个方程、k＋1个未知参数β0，β1，…，βk组成的一个线性方程组，由此可得到以下公式：

多元样本可决系数R2，也称多元样本判定系数或多元样本决定系数，是回归平方和在总离差平方和中所占的比重，是指被解释变量Y中的变异性能被估计的多元回归方程解释的比例。因为0≤RSS≤TSS，所以总有0≤R2≤1。R2的数值越接近于1，即Y中的变异性能被估计的回归方程解释的部分越多，则估计的回归方程对样本观测值就拟合得越好；反之，R2的数值越接近于0，即Y中的变异性能被估计的回归方程解释的部分越少，则估计的回归方程对样本观测值就拟合得越差。R2作为度量回归值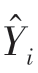对样本观测值Yi拟合优度的指标，显然R2的数值越大越好。

根据式（6.12），我们也可以将R2表示为：(www.xing528.com)

其中，

F检验，即回归方程的显著性检验，是指在一定的显著性水平下，从总体上对模型中被解释变量与解释变量之间的线性关系是否显著成立而进行的一种统计检验。F越大，显著水平越高。

为服从自由度为（k，n-k-1）的F分布。对于预先给定的显著性水平α，可从F分布表中查出相应的分子自由度为k、分母自由度为n-k-1的α水平上侧分位数Fα（k，n-k-1）。若F＞Fα（k，n-k-1），则认为总体回归方程存在显著的线性关系，否则，即认为总体回归方程不存在显著的线性关系。

t检验——解释变量的显著性检验，是指在一定的显著性水平下，检验模型的解释变量是否对被解释变量有显著影响的一种统计检验。对于多元线性回归模型，总体回归方程线性关系的显著并不意味着每个解释变量X1，X2，…，Xk对被解释变量Y的影响都是显著的。

服从自由度为（n-k-1）的t分布，其中S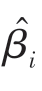（）是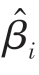标准差的估计量。对于预先给定的显著性水平α，可从t分布表中查出相应的自由度为f＝n-k-1，α水平的双侧分位数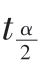（f）。如果计算出的结果有绝对值ti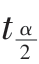＞（f），则认为解释变量Xi对被解释变量Y存在显著的影响；否则，即认为解释变量Xi对被解释变量Y不存在显著影响。