【教学目标】
1.理解分数指数的概念,掌握有理指数幂的运算性质.
(1)理解n次方根,n次根式的概念及其性质,能根据性质进行相应的根式计算.
(2)能认识到分数指数是指数概念由整数向有理数的一次推广,了解它是根式的一种新的写法,能正确进行根式与分数指数幂的互化.
(3)能利用有理指数运算性质简化根式运算.
2.通过指数范围的扩大,使学生能理解运算的本质,认识到知识之间的联系和转化,认识到符号化思想的重要性,在抽象的符号或字母的运算中提高运算能力.
3.通过对根式与分数指数幂的关系的认识,使学生能学会透过表面去认清事物的本质.
【教学建议】
教材分析
(1)本节的教学重点是分数指数幂的概念及其运算性质.教学难点是根式的概念和分数指数幂的概念.
(2)由于分数指数幂的概念是借助n次方根给出的,而n次根式,n次方根又是学生刚刚接触到的概念,也是比较陌生的.以此为基础去学习认识新知识自然是比较困难的.且n次方根,分数指数幂的定义都是用抽象字母和符号的形式给出的,学生在接受理解上也是比较困难的.基于以上原因,根式和分数指数幂的概念成为本节应突破的难点.
(3)学习本节主要目的是将指数从整数指数推广到有理数指数,为指数函数的研究作好准备.且有理指数幂具备的运算性质还可以推广到无理指数幂,也就是说在运算上已将指数范围推广到了实数范围,为对数运算的出现作好了准备,而使这些成为可能的就是分数指数幂的引入.
教法建议
(1)根式概念的引入是本节教学的关键.为了让学生感到根式的学习是很自然也很必要的,不妨在设计时可以考虑以下几点:
①先以具体数字为例,复习正整数幂,介绍各部分的名称及运算的本质是乘方,让它与学生熟悉的运算联系起来,树立起转化的观点.
②当复习负指数幂时,由于与乘除共同有关,所以出现了分式,这样为分数指数幂的运算与根式相关作好准备.
③在引入根式时可先由学生知道的平方根和立方根入手,再大胆写出?4=16即谁的四次方根等于16.指出2和-2是它的四次方根后再把指数换成n,写成?n=a即谁的n次方等于a,在语言描述的同时,也把数学的符号语言自然的给出.
(2)在n次方根的定义中并没有将n次方根符号化原因是结论的多样性,不能乱表示,所以需要先研究规律,再把它符号化.按这样的研究思路学生对n次方根的认识逐层递进,直至找出运算上的规律.
【教学设计示例】
第五节 课题根式
教学目标:
1.理解n次方根和n次根式的概念及其性质,能根据性质进行简单的根式计算.
2.通过对根式的学习,使学生能进一步认清各种运算间的联系,提高归纳,概括的能力.
3.通过对根式的化简,使学生了解由特殊到一般的解决问题的方法,渗透分类讨论的思想.
教学重点难点:
重点是n次方根的概念及其取值规律.
难点是n次方根的概念及其运算根据的研究.
教学用具:投影仪
教学方法:启发探索式.
教学过程:
一、复习引入
今天我们将学习新的一节指数.指数与其说它是一个概念,不如说它是一种重要的运算,且这种运算在初中曾经学习过,今天只不过把它进一步向前发展.
下面从我们熟悉的指数的复习开始.能举一个具体的指数运算的例子吗?
以24=16为例,是指数运算要求学生指明各部分的名称,其中2称为底数,4为指数,24称为幂.
教师还可引导学生回顾指数运算的由来,是从乘方而来,因此最初指数只能是正整数,同时引出正整数指数幂的定义.![]() .然后继续引导学生回忆零指数幂和负整数指数幂的定义,分别写出a0=0(a≠0)及a-n=
.然后继续引导学生回忆零指数幂和负整数指数幂的定义,分别写出a0=0(a≠0)及a-n=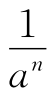 (a≠0,n∈N+),同时追问这里a≠0的由来.最后将三条放在一起,用投影仪打出整数指数幂的概念
(a≠0,n∈N+),同时追问这里a≠0的由来.最后将三条放在一起,用投影仪打出整数指数幂的概念
2.5指数(板书)
1.关于整数指数幂的复习
(1)概念
既然是一种运算,除了定义之外,自然要给出它的运算规律,再来回顾一下关于整数指数幂的运算性质.可以找一个学生说出相应的运算性质,教师用投影仪依次打出:
(2)运算性质:an·am=am+n;(am)n=amn;(ab)n=an·bn.
复习后直接提出新课题,今天在此基础上把指数从整数范围推广到分数范围.在刚才的复习我们已经看到当指数在整数范围内时,运算最多也就是与分式有关,如果指数推广到分指数会与什么有关呢?应与根式有关.初中时虽然也学过一点根式,但不够用,因此有必要先从根式说起.
2.根式(板书)
我们知道根式来源于开方,开方是乘方的逆运算,所以谈根式还是先从大家熟悉的乘方说起.
如42=16
如果给出了4和2进行运算,那就是乘方运算.如果是知道了16和2,求4即?2=16,求?
问题也就是:谁的平方是16,大家都能回答是4和-4,这就是开方运算,且4和-4有个名字叫16的平方根.
再如23=8
知3和8,问题就是谁的立方是8?这就是开方运算,大家也知道结果为2,同时指出2叫做8的立方根.
(根据情况教师可再适当举几个例子,如?4=9,?3=-8,要求学生用语言描述式子的含义,I再说出结果分别为±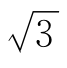 和-2,同时指出它们分别称为9的四次方根和-8的立方根)
和-2,同时指出它们分别称为9的四次方根和-8的立方根)
在以上几个式子会解释的基础上,提出?n=a即一个数的n次方等于a,求这个数,即开n次方,那么这个数叫做a的n次方根.
(1)n次方根的定义:如果一个数的n次方等于a(n>1,n∈N+那么这个数叫做a的n次方根.
(板书)
对定义理解的第一步就是能把上述语言用数学符号表示,请同学们试试看.
由学生翻译为:若xn=a(n>1,n∈N+),则x叫做a的n次方根.(把它补在定义的后面)
翻译后教师在此基础上再次提出翻译的不够彻底,如结论中的a的n次方根就没有用符号表示,原因是什么?(如果学生不知从何入手,可引导学生回到刚才的几个例子,在符号表示上存在的问题,并一起研究解决的办法)最终把问题引向对a的n次方根的取值规律的研究.
(2)a的n次方根的取值规律:(板书)
先让学生看到a的n次方根的个数是由n的奇偶性决定的,所以应对n分奇偶情况讨论
当n为奇数时,再问学生a的n次方根是个什么样的数,与谁有关,再提出对a的正负的讨论,从而明确分类讨论的标准,按a的正负分为三种情况.
Ⅰ当n为奇数时
a>0,a的n次方根为一个正数;
a<0,a的n次方根为一个负数;
a=0,a的n次方根为零.(板书)
当奇数情况讨论完之后,再用几个具体例子辅助说明n为偶数时的结论,再由学生总结归纳
Ⅱ当n为偶数时
a>0,a的n次方根为两个互为相反数的数;
a<0,a的n次方根不存在;
a=0,a的n次方根为零.
对于这个规律的总结,还可以先看a的正负,再分n的奇偶,换个角度加深理解.
有了这个规律之后,就可以用准确的数学符号去描述n次方根了.
(3)a的n次方根的符号表示(板书)
可由学生试说一说,若学生说不好,教师可与学生一起总结,当n为奇数时,由于无论a为何值,n次方根都只有一个值,可用统一的符号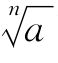 表示,此时要求学生解释符号的含义:a为正数,则
表示,此时要求学生解释符号的含义:a为正数,则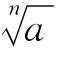 为一个确定的正数,a为负数,则
为一个确定的正数,a为负数,则 为一个确定的负数,a为零,则
为一个确定的负数,a为零,则 为零.
为零.
当n为偶数时,a为正数时,有两个值,而 只能表示其中一个且应表示是正的,另一个应与它互为相反数,故只需在前面放一个负号,写成
只能表示其中一个且应表示是正的,另一个应与它互为相反数,故只需在前面放一个负号,写成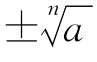 ,其含义为n为偶数时,正数的n次方根有两个分别为
,其含义为n为偶数时,正数的n次方根有两个分别为 和
和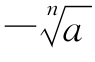 .(https://www.xing528.com)
.(https://www.xing528.com)
为了加深对符号的认识,还可以提出这样的问题: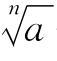 一定表示一个正数吗?
一定表示一个正数吗? 中的a一定是正数或非负数吗?让学生来回答,在回答中进一步认清符号的含义,再从另一个角度进行总结
中的a一定是正数或非负数吗?让学生来回答,在回答中进一步认清符号的含义,再从另一个角度进行总结 .对于符号
.对于符号 ,当n为偶数是,它有意义的条件是a≥0;当n为奇数时,它有意义的条件时a∈R.
,当n为偶数是,它有意义的条件是a≥0;当n为奇数时,它有意义的条件时a∈R.
把 称为根式,其中n为根指数,a叫做被开方数.(板书)
称为根式,其中n为根指数,a叫做被开方数.(板书)
(4)根式运算的依据(板书)
由于 是个数值,数值自然要进行运算,运算就要有根据,因此下面有必要进一步研究根式运算的依据.但我们并不过分展开,只研究一些最基本的最简单的依据.
是个数值,数值自然要进行运算,运算就要有根据,因此下面有必要进一步研究根式运算的依据.但我们并不过分展开,只研究一些最基本的最简单的依据.
如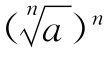 应该得什么?有学生讲出理由,根据n次方根的定义,可得Ⅰ
应该得什么?有学生讲出理由,根据n次方根的定义,可得Ⅰ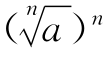 =a.(板书)
=a.(板书)
再问: 应该得什么?也得a吗?
应该得什么?也得a吗?
若学生想不清楚,可用具体例子提示学生,如![]() =-4吗?
=-4吗?![]() 吗?让学生能发现结果与有关,从而得到Ⅱ
吗?让学生能发现结果与有关,从而得到Ⅱ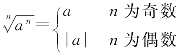 .(板书)
.(板书)
为进一步熟悉这个运算依据,下面通过练习来体会一下.
三.巩固练习
例1 求值
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)
![]()
要求学生口答,并说出简要步骤.
四.小结
1.n次方根与n次根式的概念
2.二者的区别
3.运算依据
五.作业 略
六.板书设计
【习题精选】
(1)式子![]() 经过计算可得到( ).
经过计算可得到( ).
(2)给出下列四个算式及运算结果:
其中正确的有( )
(A)1个 (B)2个
(C)3个 (D)4个
(3)要使式子![]() 有意义,则x的取值范围是__________.
有意义,则x的取值范围是__________.
(4)若![]() 则(x+
则(x+![]() 的值是___________.
的值是___________.
(5)![]() 化成分数指数幂得__________.
化成分数指数幂得__________.
(6)化简
①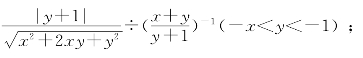
②![]()
(7)计算求值
①![]()
②
③![]()
(8)若102x=25则101-x的值为___________.
(9)若![]() ,则
,则![]() 的值为__________.
的值为__________.
(10)已知![]() ,求
,求![]() 的值.
的值.
答案:
(1)D (2)A (3)(-∞,-3)∪(-1,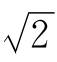 )∪(
)∪(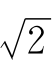 ,+∞) (4)8 (5
,+∞) (4)8 (5 (6)①-1;②
(6)①-1;②![]() (7)①
(7)①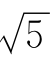 ;②
;② ;③
;③ (8)2 (9)
(8)2 (9) -1 (10
-1 (10
【典型例题】
例1 下列说法中正确的是( ).
(A)-2是16的四次方根
(B)正数的n次方根有两个
(C)a的n次方根就是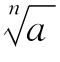
(D) =a(a≥0)
=a(a≥0)
分析:从n次方根和n次根式的概念入手,认清各概念与各符号之间的关系.
解:(1)是正确的.由(-2)4=16可验证.
(2)不正确,要对n分奇偶讨论.
(3)不正确,a的n次方根可能有一个值,可能有两个值,而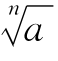 只表示一个确定的值它叫根式.
只表示一个确定的值它叫根式.
(4)正确,根据根式运算的依据,当n为奇数时, =a是正确的,当n为偶数时,若a≥0,则有
=a是正确的,当n为偶数时,若a≥0,则有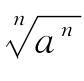 =a,综上,当a≥0时,无论n为何值均有
=a,综上,当a≥0时,无论n为何值均有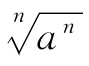 =a成立.
=a成立.
说明:此题主要目的是分清n次方根是什么和有几个,进一步明确根式进行简单运算的依据.
例2 求下列各式的值.
分析:依照根式运算的两条规律,进行运算即可.
解:(1)![]()
(2)![]()
(3)![]()
(4)![]()

说明:根式运算要注意分清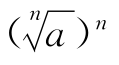 与
与 ,此外对于
,此外对于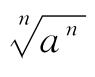 的运算可以记为
的运算可以记为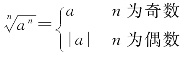 ,这样先根据n的奇偶处理根式,再根据a的正负处理绝对值比较方便.
,这样先根据n的奇偶处理根式,再根据a的正负处理绝对值比较方便.
例3 求下列各式的值.
(1)![]()
(2)![]()
![]()
(3)![]()
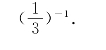
分析:依照分数指数幂的运算法则,并结合概念来完成运算.
解:(1)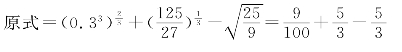
![]()
(2)![]()
![]()
(3)
说明:在分数指数幂的运算中要注意把法则和概念结合起来,进行运算,并能根据具体题目选择最恰当的形式来完成运算.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




