【教学目标】
(1)正确理解充分条件、必要条件和充要条件的概念;
(2)能正确判断是充分条件、必要条件还是充要条件;
(3)培养学生的逻辑思维能力及归纳总结能力;
(4)在充要条件的教学中,培养等价转化思想.
【教学建议】
教材分析
知识结构
首先给出推断符号“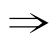 ”,并引出充分条件与必要条件的意义,在此基础上讲述了充要条件的初步知识.
”,并引出充分条件与必要条件的意义,在此基础上讲述了充要条件的初步知识.
重点难点分析
本节的重点与难点是关于充要条件的判断.
(1)充分但不必要条件、必要但不充分条件、充要条件、既不充分也不必要条件是重要的数学概念,主要用来区分命题的条件p和结论q之间的因果关系.
(2)在判断条件p和结论q之间的因果关系中应该:
①首先分清条件是什么,结论是什么;
②然后尝试用条件推结论,再尝试用结论推条件.推理方法可以是直接证法、间接证法(即反证法),也可以举反例说明其不成立;
③最后再指出条件是结论的什么条件.
(3)在讨论条件p和条件q的关系时,要注意:
①若p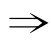 q,但q
q,但q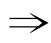 p,则p是q的充分但不必要条件;
p,则p是q的充分但不必要条件;
②若q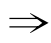 p,但p
p,但p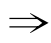 q,则p是q的必要但不充分条件;
q,则p是q的必要但不充分条件;
③若p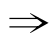 q,且q
q,且q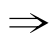 p,则p是q的充要条件;
p,则p是q的充要条件;
④若p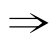 q,且﹁p
q,且﹁p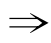 ﹁q,则p是q的充要条件;
﹁q,则p是q的充要条件;
⑤若p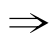 q,且q
q,且q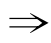 p,则p是q的既不充分也不必要条件.
p,则p是q的既不充分也不必要条件.
(4)若条件p以集合A的形式出现,结论q以集合B的形式出现,则借助集合知识,有助于充要条件的理解和判断.
①若A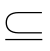 B,则p是q的充分条件;
B,则p是q的充分条件;
显然,要使元素x∈B,只需就够了x∈A.类似地还有:
②若A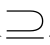 B,则p是q的必要条件;
B,则p是q的必要条件;
③若A=B,则p是q的充要条件;
④若A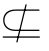 B,且A
B,且A B,则p是q的既不必要也不充分条件.
B,则p是q的既不必要也不充分条件.
(5)要证明命题的条件是充要条件,就既要证明原命题成立,又要证明它的逆命题成立.证明原命题即证明条件的充分性,证明逆命题即证明条件的必要性.由于原命题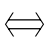 逆否命题,逆命题
逆否命题,逆命题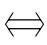 否命题,当我们证明某一命题有困难时,可以证明该命题的逆否命题成立,从而得出原命题成立.
否命题,当我们证明某一命题有困难时,可以证明该命题的逆否命题成立,从而得出原命题成立.
教法建议
1.学习充分条件、必要条件和充要条件知识,要注意与前面有关逻辑初步知识内容相联系.充要条件中的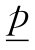 ,
,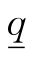 与四种命题中的p,q要求是一样的.它们可以是简单命题,也可以是不能判断真假的语句,也可以是含有逻辑联结词或“若a则b”形式的复合命题.
与四种命题中的p,q要求是一样的.它们可以是简单命题,也可以是不能判断真假的语句,也可以是含有逻辑联结词或“若a则b”形式的复合命题.
2.由于这节课概念性、理论性较强,一般的教学使学生感到枯燥乏味,为此,激发学生的学习兴趣是关键.教学中始终要注意以学生为主,让学生在自我思考、相互交流中去结概念“下定义”,去体会概念的本质属性.
3.由于“充要条件”与命题的真假、命题的条件与结论的相互关系紧密相关,为此,教学时可以从判断命题的真假入手,来分析命题的条件对于结论来说,是否充分,从而引入“充分条件”的概念,进而引入“必要条件”的概念.
4.教材中对“充分条件”、“必要条件”的定义没有作过多的解释说明,为了让学生能理解定义的合理性,在教学过程中,教师可以从一些熟悉的命题的条件与结论之间的关系来认识“充分条件”的概念,从互为逆否命题的等价性来引出“必要条件”的概念.
【教学设计示例】
充要条件
教学目标:
(1)正确理解充分条件、必要条件和充要条件的概念;
(2)能正确判断是充分条件、必要条件还是充要条件;
(3)培养学生的逻辑思维能力及归纳总结能力;
(4)在充要条件的教学中,培养等价转化思想.
教学重点难点:关于充要条件的判断
教学用具:幻灯机或实物投影仪
教学过程设计
1.复习引入
练习:判断下列命题是真命题还是假命题(用幻灯投影):
(1)若x≥1,则x2≥1;
(2)若x2=y2,则x=y;
(3)全等三角形的面积相等;
(4)对角线互相垂直的四边形是菱形;
(5)若ab=0,则a=0;
(6)若方程ax2+bx+c=0(a≠0)有两个不等的实数解,则b2-4ac>0.
(学生口答,教师板书.)
(1)、(3)、(6)是真命题,(2)、(4)、(5)是假命题.
置疑:对于命题“若p,则q”,有时是真命题,有时是假命题.如何判断其真假的?
答:看p能不能推出q,如果p能推出q,则原命题是真命题,否则就是假命题.
对于命题“若p,则q”,如果由p经过推理能推出q,也就是说,如果p成立,那么一定成立.换句话说,只要有条件就能充分地保证结论的成立,这时我们称条件是成立的充分条件,记作p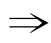 q.
q.
2.讲授新课
(板书充分条件的定义.)
一般地,如果已知p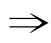 q,那么我们就说p是q成立的充分条件.
q,那么我们就说p是q成立的充分条件.
提问:请用充分条件来叙述上述(1)、(3)、(6)的条件与结论之间的关系.
(学生口答)
(1)“x≥1,”是“x2≥1”成立的充分条件;
(2)“三角形全等”是“三角形面积相等”成立的充分条件;
(3)“方程ax2+bx+c=0(a≠0)的有两个不等的实数解”是“b2-4ac>0”成立的充分条件.
从另一个角度看,如果p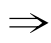 q成立,那么其逆否命题﹁p
q成立,那么其逆否命题﹁p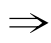 ﹁q也成立,即如果没有q,也就没有p,亦即q是p成立的必须要有的条件,也就是必要条件.
﹁q也成立,即如果没有q,也就没有p,亦即q是p成立的必须要有的条件,也就是必要条件.
(板书必要条件的定义.)
提出问题:用“充分条件”和“必要条件”来叙述上述6个命题.
(学生口答).
(1)因为x≥1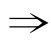 x2≥1,所以x≥1是x2≥1的充分条件,x2≥1是x≥1的必要条件;
x2≥1,所以x≥1是x2≥1的充分条件,x2≥1是x≥1的必要条件;
(2)因为x2=y2 x=y,所以x2=y2是x=y的必要条件,x=y是x2=y2的充分条件;
x=y,所以x2=y2是x=y的必要条件,x=y是x2=y2的充分条件;
(3)因为“两三角形全等”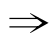 “两三角形面积相等”,所以“两三角形全等”是“两三角形面积相等”的充分条件,“两三角形面积相等”是“两三角形全等”的必要条件;
“两三角形面积相等”,所以“两三角形全等”是“两三角形面积相等”的充分条件,“两三角形面积相等”是“两三角形全等”的必要条件;
(4)因为“四边形的对角线互相垂直”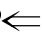 “四边形是菱形”,所以“四边形的对角线互相垂直”是“四边形是菱形”的必要条件,“四边形是菱形”是“四边形的对角线互相垂直”的充分条件;
“四边形是菱形”,所以“四边形的对角线互相垂直”是“四边形是菱形”的必要条件,“四边形是菱形”是“四边形的对角线互相垂直”的充分条件;
(5)因为ab=0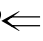 a=0,所以ab=0是a=0的必要条件,a=0是ab=0的充分条件;
a=0,所以ab=0是a=0的必要条件,a=0是ab=0的充分条件;
(6)因为“方程ax2+bx+c=0(a≠0)的有两个不等的实根”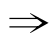 “b2-4ac>0”,而且“方程ax2+bx+c=0(a≠0)的有两个不等的实根”
“b2-4ac>0”,而且“方程ax2+bx+c=0(a≠0)的有两个不等的实根”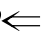 “b2-4ac>0”,所以“方程ax2+bx+c=0(a≠0)的有两个不等的实根”是“b2-4ac>0”充分条件,而且是必要条件.
“b2-4ac>0”,所以“方程ax2+bx+c=0(a≠0)的有两个不等的实根”是“b2-4ac>0”充分条件,而且是必要条件.
总结:如果p是q的充分条件,p又是q的必要条件,则称p是q的充分必要条件,简称充要条件,记作p q.
q.
(板书充要条件的定义.)
3.巩固新课
例1 (用投影仪投影.)
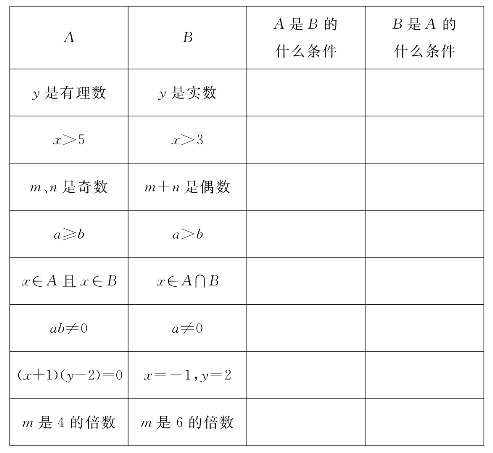
(学生活动,教师引导学生作出下面回答.)
①因为有理数一定是实数,但实数不一定是有理数,所以A是B的充分非必要条件,B是A的必要非充分条件;
②x>5一定能推出x>3,而x>3不一定推出x>5,所以A是B的充分非必要条件,B是A的必要非充分条件;
③m、n是奇数,那么m+n一定是偶数;m+n是偶数,m、n不一定都是奇数(可能都为偶数),所以A是B的充分非必要条件,B是A的必要非充分条件;
④a≥b表示a>b或a=b,所以a≥b是a>b成立的必要非充分条件;
⑤由交集的定义可知x∈A且x∈B是x∈A∩B成立的充要条件;
⑥由ab≠0知a≠0且b≠0,所以ab≠0是a≠0成立的充分非必要条件;
⑦由(x+1)(y-2)=0知x=-1或y=2,所以(x+1)(y-2)=0是x=-1,y=2成立的必要非充分条件;
⑧易知“m是4的倍数”是“m是6的倍数”成立的既非充分又非必要条件;
(通过对上述问题的交流、思辩,在争论中得到了正确答案,并加深了对充分条件、必要条件的认识.)
例2 已知α是β的充要条件,S是r的必要条件同时又是β的充分条件,试α与r的关系.(投影)
解:由已知得
α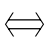 β
β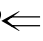 S
S r,
r,
所以r是α的充分条件,α或r是的必要条件.
4.小结回授(https://www.xing528.com)
今天我们学习了充分条件、必要条件和充要条件的概念,并学会了判断条件A是B的什么条件,这为我们今后解决数学问题打下了等价转化的基础.
课内练习:课本(人教版,试验修订本,第一册(上))第35页练习l、2;第36页练习l、2.
(通过练习,检查学生掌握情况,有针对性的进行讲评.)
5.课外作业:教材第36页
习题1.8 1、2、3.
【习题精选】
一、填空题
1.“a>b>c”是“(a-b)(b-c)(c-a)<0”的___________条件.
2.“集合A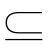 B,B
B,B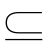 C,C
C,C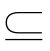 A”是“集合A=B=C”的___________条件.
A”是“集合A=B=C”的___________条件.
3.“a∈R,|a|<1”是“方程x2+(a2-1)x+a-2=0的一个根大于1,另一个根小于1”的___________条件.
二、解答题
1.指出一次函数y=-2x+a2与![]() 的图象的交点落在第一象限的充要条件.
的图象的交点落在第一象限的充要条件.
2.求关于x的一元二次不等式ax2+1>ax对于一切实数x都成立的充要条件.
【参考答案】
一、填空题
1.充分但不必要条件. 2.充要条件. 3.充分但不必要条件.提示:设f(x)=x2+(a2-1)x+a-2,则f(1)=a2+a-2<0,-2<a<1.
二、解答题
1.充要条件是![]()
2.充要条件是0<a<4
【典型例题】
例1 指出下列各组命题中,p是q的什么条件(在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种).
(1)p:四边形对角线互相平分;q:四边形是矩形.
(2)p:c=0;q:抛物线y=ax2+bx+c(a≠0)过原点.
(3)p:0<x<3;q:|x-1|<2.
(4)p:方程ax2+bx+c有一根为1;q:a+b+c=0(a,b,c,∈R).
(5)p:m>0;q:方程x2+x-m=0有实根.
(6)p:A B
B S;q(CSB
S;q(CSB CSA).
CSA).
解:(1)四边形对角线互相平分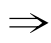 四边形是矩形.四边形是矩形
四边形是矩形.四边形是矩形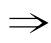 四边形对角线互相平分.所以p是q的必要而不充分条件.
四边形对角线互相平分.所以p是q的必要而不充分条件.
(2)c=0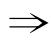 抛物线y=ax2+bx+c(a≠0)过原点,
抛物线y=ax2+bx+c(a≠0)过原点,
抛物线y=ax2+bx+c(a≠0)过原点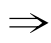 c=0.
c=0.
所以p是q的充要条件.
(3)0<x<3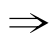 |x-1|<2,|x-1|<2
|x-1|<2,|x-1|<2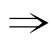 0<x<3.
0<x<3.
所以p是q的充分而不必要条件.
(4)方程有一根为.
方程ax2+bx+c=0有一根为1 a+b+c=0(a,b,c,∈R).
a+b+c=0(a,b,c,∈R).
a+b+c=0(a,b,c,∈R)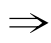 方程ax2+bx+c=0有一根为1.
方程ax2+bx+c=0有一根为1.
所以p是q的充要条件.
(5)m>0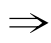 方程x2+x-m=0有实根,方程x2+x-m=0有实根
方程x2+x-m=0有实根,方程x2+x-m=0有实根 m>0.
m>0.
所以p是q的充分而不必要条件.
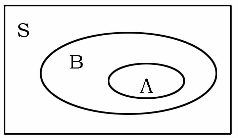
图1-13
(6)利用集合的图示法(图1—13),知
A B
B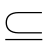 S
S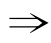 (C,B)
(C,B)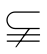 (C,A),(C,B)
(C,A),(C,B)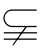 (C,A)
(C,A)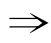 A
A B
B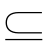 S.
S.
所以p是q的充要条件.
注意,第(5)小题也可从集合观点入手研究其充分必要性.实际上,
p:A={m∈R|m>0},
q:B={m∈R|方程x2+x-m=0有实根}=![]()
因为A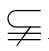 B,所以p是q的充分而不必要条件.请用集合观点解答第(3)小题.
B,所以p是q的充分而不必要条件.请用集合观点解答第(3)小题.
例2 已知关于x的一元二次方程(m∈Z)
mx2-4x+4=0 ①
x2-4mx-4m2-4m-5=0 ②
求方程①和②的根都是整数的充要条件.
解:方程①有实数根的充要条件是△=16-4·4·m≥0,解得m≤1;
方程②有实数根的充要条件是△16m2-4(4m2-4m-5)≥0,解得m≥-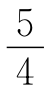 .
.
所以-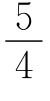 ≤m≤1.而m∈Z,得m=-1,或m=0,或m=1.
≤m≤1.而m∈Z,得m=-1,或m=0,或m=1.
当m=-1时,方程①为x2+4x-4=0,无整数根;
当m=0时,方程②为x2-5=0,无整数根;
当m=1时,方程①为x2+4x+4=0,方程②为x2+4x-5=0,①和②的根都是整数.
从而,①和②的根都是整数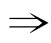 m=1;反之,
m=1;反之,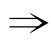 m=1①和②的根都是整数.
m=1①和②的根都是整数.
所以方程①和②的根都是整数的充要条件是m=1.
例3 设关于x的一元二次不等式,mx2-mx+1>0对一切实数均成立,求m的取值范围.
解:一元二次不等式mx2-mx+1>0,对一切x∈R恒成立 二次函数y=mx2-mx+1的图像全在x轴上方
二次函数y=mx2-mx+1的图像全在x轴上方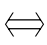
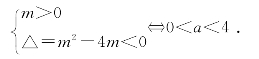
注:这里“m的取值范围:0<m<4”就是“二次不等式mx2-mx+1>0对一切实数x都成立”的充要条件.
有些问题(如求字母m的取值范围),我们必须通过等价变换,才能获得正确结果,这里的“等价变换”与“充要条件”是紧密相连的.我们所熟悉的解方程(或不等式)的过程,实质上是等价变换的过程.
例4 “p且q为真”是“p或q为真”的( )
(A)充分不必要条件.
(B)必要不充分条件.
(C)充要条件.
(D)既不充分又不必要条件.
解:“p且q为真”,就是p和q都为真,所以p或q为真,即p且q为真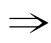 p或q为真.
p或q为真.
“p或q为真”,即p为真或q为真,p与q不一定同时为真,所以,p或q为真 p且q为真.
p且q为真.
所以“p且q为真”是“p或q为真”的充分不必要条件.
例5 若甲是乙的充分条件,乙是丙的充要条件,丙是丁的必要条件,丁是乙的必要条件,问甲是丙的什么条件?乙是丁的什么条件?
解:由题意,分析如下图所示.
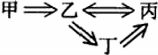
根据图示得:甲是丙的充分条件,乙是丁的充要条件.
常见错误及分析:
错解1:由图知,甲是丙的充分不必要条件,产生错误的原因是把“甲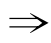 乙”理解成了
乙”理解成了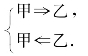
错解2:判为“乙是丁的充分条件”.产生错误的原因是只看出“乙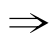 丁”,而没有根据推理“丁
丁”,而没有根据推理“丁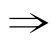 丙
丙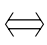 乙”得出“丁
乙”得出“丁 乙”.
乙”.
例6已知p:-2≤x≤10;q:1-m≤x≤1+m(m>0).若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
点拨:可以有两个思路:
(1)先求出﹁p和﹁q,然后根据﹁p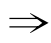 ﹁q,﹁q
﹁q,﹁q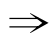 ﹁p,求得m的取值范围;
﹁p,求得m的取值范围;
(2)若原命题为“若﹁q,则﹁p”,其逆否命题是“若p则q”,由于它们是等价的,可以把求﹁p是﹁p的必要而不充分条件等价转换为求p是q的充分而不必要条件.
解法一:求出﹁p:A={x∈R|x>0,或x<-2},
﹁q:B={x∈R|x>1+m,或x<1-m,m>0}.
由﹁p是﹁q的必要而不充分条件,知B A,
A,
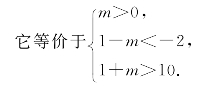
同样解得 的取值范围是m>9.
解法二:根据思路二,﹁p是﹁q的必要而不充分条件,等价于p是q的充分而不必要条件.设
p:A={x∈R|-2≤x≤10};
q:B={x∈R|1-m≤x≤1+m,m>0};
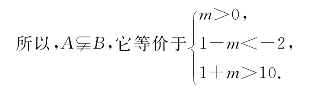
同样解得m的取值范围是m>9.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




