高一数学：逻辑联结词及命题概念简介

【教学目标】

（1）了解含有“或”、“且”、“非”复合命题的概念及其构成形式；

（2）理解逻辑联结词“或”“且”“非”的含义；

（3）能用逻辑联结词和简单命题构成不同形式的复合命题；

（4）能识别复合命题中所用的逻辑联结词及其联结的简单命题；

（5）会用真值表判断相应的复合命题的真假；

（6）在知识学习的基础上，培养学生简单推理的技能．

【教学建议】

教材分析

知识结构

重点难点分析

重点是判断复合命题真假的方法；难点是对“或”的含义的理解．

（1）复合命题

含“或”、“且”、“非”的命题有的不是复合命题．如：（1）实数的平方是正数或零；（2）若x＞1或x＜－1，则x＞0．

不含“或”、“且”、“非”的命题有可能是复合命题．如：（3）3≥2；（4）有两个解为45°的三角形是等腰直角三角形．

所以，判断一个命题是否为“或”命题、“且”命题、“非”命题，既要看它是否含有“或”、“且”、“非”，又要看它是否隐含着“或”、“且”、“非”，还要看“或”、“且”、“非”是否为两个命题之间的联结词或某一命题的否定；既要与集合运算中的“并”、“交”、“补”联系起来，又要与“或”、“且”、“非”命题的真值表联系起来；既要看原命题，又要看它的等值命题．

（2）真值表是根据简单命题的真假，判断由这些简单命题与逻辑联结词构成的复合命题的真假的工具，它并不涉及简单命题之间的具体内容．例如，已知命题p为“0是自然数”，命题q为“三角形的二边之和小于第三边”，尽管p和q的具体内容毫无相干，但仍不妨碍我们讨论和判断“p或q”、“p且q”的真假，也不妨碍我们接受p真q假则“p或q”为真、“p且q”为假的结论，这里特别要注意对“或”的理解．

（3）要在理解的基础上记忆三个真值表：

（3）要在理解的基础上记忆三个真值表：

为了正确判断复合命题的真假，首先应该确定复合命题的形式，然后指出其中简单命题的真假，再根据真值表判断这个复合命题的真假．

教法建议

1．从学生在初中熟悉的一些例子引入，如：“三角形的中位线平行于第三边”是简单命题；“菱形的对角线互相垂直且平分”是“p且q”形式的复合命题；“不等式（a－b）2≥0”是“p或q”形式的复合命题，“π非有理数”是“非p”形式的复合命题．

在开始先给学生一个似乎熟悉的印象，学生容易接受，使得逻辑联结词这一节抽象的数学概念由易到难，逐步深入理解．

2．学习本节内容时，可以运用复合命题的结构形式，分析初中学过的一些定义和定理，既可加深对逻辑联结词的理解，增强对复合命题的认识，又可体现初、高中知识的衔接和知识连贯性与实用性．

3．教科书中，三个真值表是按先易后难顺序编排的．先讲“非p”形式复合命题的真假，再讲“p且q”形式复合命题的真假，“p或q”形式复合命题的真假理解起来最困难，放后面讲．

4．在讲述逻辑联结词“或”、“且”、“非”时，可以适当联系集合中的“并集”、“交集”、“补集”的概念，实际上它们的密切的关系．例如，并集、交集、补集的定义分别是：

A∪B＝｛x｜x∈A或x∈B｝；A∩B＝｛x｜x∈A且x∈B｝；CSA＝｛x∈S｜xA｝

5．对逻辑联结词“或”、“且”、“非”的理解，与判断复合命题真假分不开的．逻辑中的“或”、“且”、“非”与日常用语中的“或”、“且”、“非”的意义是不尽相同的，要直接讲清楚它们的意义，比较困难，例如，像3≥3与3≥2的关系式，初接触时，学生可能不容易接受．因此，开始时，不必深讲，可以在学习了有关复合命题的真值表之后，再要求学生根据复合命题的真值表，对“或”、“且”、“非”加以理解．

【教学设计方案】

第六节　逻辑联结词

教学目标

（1）了解含有“或”、“且”、“非”复合命题的概念及其构成形式；

（2）理解逻辑联结词“或”“且”“非”的含义；

（3）能用逻辑联结词和简单命题构成不同形式的复合命题；

（4）能识别复合命题中所用的逻辑联结词及其联结的简单命题；

（5）会用真值表判断相应的复合命题的真假；

（6）在知识学习的基础上，培养学生简单推理的技能．

教学重点难点：

重点是判断复合命题真假的方法；难点是对“或”的含义的理解．

教学过程

1．新课导入

在当今社会中，人们从事任何工作、学习，都离不开逻辑．具有一定逻辑知识是构成一个公民的文化素质的重要方面．数学的特点是逻辑性强，特别是进入高中以后，所学的教学比初中更强调逻辑性．如果不学习一定的逻辑知识，将会在我们学习的过程中不知不觉地经常犯逻辑性的错误．其实，同学们在初中已经开始接触一些简易逻辑的知识．

初一平面几何中曾学过命题，请同学们举一个命题的例子．（板书：命题．）

（从初中接触过的“命题”入手，提出问题，进而学习逻辑的有关知识．）

学生举例：平行四边形的对角线互相平．……（1）

两直线平行，同位角相等．…………（2）

教师提问：“……相等的角是对顶角”是不是命题？……（3）

（同学议论结果，答案是肯定的．）

教师提问：什么是命题？

（学生进行回忆、思考．）

概念总结：对一件事情作出了判断的语句叫做命题．

（教师肯定了同学的回答，并作板书．）

由于判断有正确与错误之分，所以命题有真假之分，命题（1）、（2）是真命题，而（3）是假命题．

（教师利用投影片，和学生讨论以下问题．）

例1　判断以下各语句是不是命题，若是，判断其真假：

答　案

1．对顶角相等；　（真命题）

2．内错角相等；　（假命题）

3．画线段AB＝CD；　（不是命题）

4．对顶角相等吗？　（不是命题）

命题一定要对一件事情作出判断，（3）、（4）没有对一件事情作出判断，所以它们不是命题．

初中所学的命题概念涉及逻辑知识，我们今天开始要在初中学习的基础上，介绍简易逻辑的知识．

2．讲授新课

大家看课本（人教版，试验修订本，第一册（上））从第25页至26页例1前，并归纳一下这段内容主要讲了哪些问题？

（片刻后请同学举手回答，一共讲了四个问题．师生一道归纳如下．）

（1）什么叫做命题？

可以判断真假的语句叫做命题．

判断一个语句是不是命题，关键看这语句有没有对一件事情作出了判断，疑问句、祈使句都不是命题．有些语句中含有变量，如x2－5x＋6＝0中含有变量x，在不给定变量的值之前，我们无法确定这语句的真假（这种含有变量的语句叫做“开语句”）．

（2）介绍逻辑联结词“或”、“且”、“非”．

“或”、“且”、“非”这些词叫做逻辑联结词．逻辑联结词除这三种形式外，还有“若…则…”和“当且仅当”两种形式．

对“或”的理解，可联想到集合中“并集”的概念．A∪B＝｛x｜x∈A，或x∈B｝中的“或”，它是指“x∈A”、“x∈B”中至少一个是成立的，即x∈A且xB；也可以x∈B且xA；也可以x∈A且x∈B．这与生活中“或”的含义不同，例如“你去或我去”，理解上是排斥你我都去这种可能．

对“且”的理解，可联想到集合中“交集”的概念．A∪B＝｛x｜x∈A，且x∈B｝中的“且”，是指“x∈A”、“x∈B这两个条件都要满足的意思．

对“非”的理解，可联想到集合中的“补集”概念，若命题P对应于集合P，则命题非P就对应着集合P在全集U中的补集CUP．

（3）

命题可分为简单命题和复合命题．

不含逻辑联结词的命题叫做简单命题．简单命题是不含其他命题作为其组成部分（在结构上不能再分解成其他命题）的命题．

由简单命题和逻辑联结词构成的命题叫做复合命题，如“6是自然数且是偶数”就是由简单命题“6是自然数”和“6是偶数”由逻辑联结词“且”构成的复合命题．

（4）命题的表示：用p，q，r，s，……来表示．

（教师根据学生回答的情况作补充和强调，特别是对复合命题的概念作出分析和展开．）

我们接触的复合命题一般有“p或q”、“p且q”、“非p”、“若p则q”等形式．

给出一个含有“或”、“且”、“非”的复合命题，应能说出构成它的简单命题和弄清它所用的逻辑联结词；应能根据所给出的两个简单命题，写出含有逻辑联结词“或”、“且”、“非”的复合命题．

对于给出“若p则q”形式的复合命题，应能找到条件p和结论q．

在判断一个命题是简单命题还是复合命题时，不能只从字面上来看有没有“或”、“且”、“非”．例如命题“等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合”，此命题字面上无“且”；命题“5的倍数的末位数字不是0就是5”的字面上无“或”，但它们都是复合命题．

3．巩固新课

例2　判断下列命题，哪些是简单命题，哪些是复合命题．如果是复合命题，指出它的构成形式以及构成它的简单命题．

（1）12≥5；

（2）0．5非整数；

（3）内错角相等，两直线平行；

（4）菱形的对角线互相垂直且平分；

（5）平行线不相交；

（6）若ab＝0，则a＝0．

（让学生有充分的时间进行辨析．教材中对“若…则…”不作要求，教师可以根据学生的情况作些补充．）

例3　写出下表中各给定语的否定语（用课件打出来）．

分析：“等于”的否定语是“不等于”；

“大于”的否定语是“小于或者等于”；

“是”的否定语是“不是”；

“都是”的否定语是“不都是”；

“至多有一个”的否定语是“至少有两个”；

“至少有一个”的否定语是“一个都没有”；

“至多有n个”的否定语是“至少有n＋1个”．

（如果时间宽裕，可让学生讨论后得出结论．）(www.xing528.com)

置疑：“或”、“且”的否定是什么？（视学生的情况、课堂时间作适当的辨析与展开．）

4．课堂练习：第26页练习1，2．

5．课外作业：第29页习题1．61，2．

【习题精选】

一、填空题

1．如果命题“p且q”与命题“非p”都是假命题，那么命题q一定是__________．

2．举一个反例，说明命题“方程的解集是R”是假命题：__________．

3．命题“x＝±2都能使有意义”是__________形式的复合命题，用真值表判断，它是__________命题．

二、解答题

1．分别指出由下列命题构成的“p或q”、“p且q”、“非p”形式复合命题的真假：

p：由澳门回归祖国的日期组成的数19991220是3的倍数；

q：由澳门回归祖国的日期组成的数19991220是4的倍数．

2．命题“π≥3”是由哪两个p，q构成的什么形式的命题？判断此命题的真假．

【参考答案】

一、填空题

1．假命题．　2．如x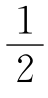＝－，则方程无意义．　3．p或q；真．

二、解答题

1．“p或q”、“p且q”都为真，“非p”为假．

2．p：π＞3；q：π＝3“p或q”是真命题

【典型例题】

例1　下列语句中，哪些是命题？哪些不是命题？

（1）若xy＝0，则x＝0，且y＝0；

（2）若x2＋y2＝0，则x＝0，且y＝0；

（3）任何集合都有一个子集；

（4）若x＝5，或x＝－4，则（x－5）（x＋4）＝0；

（5）x2－9≥0．

解：（1）由xy＝0，只能推出x＝0，或y＝0．x＝0，且y＝0不一定成立．所以此语句是假的，则它是命题．

（2）由x2＋y2＝0，则得x与y必同时为0（若x、y中至少有一个不为0，那么x2＋y2＞0），即x＝0且y＝0．此语句为真，则它是命题．

（3）因为空集是任何集合的子集，所以任何一个集合必有一个子集Ø．此语句为真，则是命题．

（4）由x＝5，或x＝－4都能推出（x－5）（x＋4）＝0，所以此语句为真，则是命题．

（5）因为x2－9与0的关系随x取值的变化而变化，所以不能判断x2－9＞0的真假，则不是命题．

例2　分别指出由下列命题构成的“p或q”“p且q”“非p”形式复命题的真假：

（1）p：x2＋1≥1；q：3＞4

（2）p：3是163的约数；q：－3是方程x2＋5x＋6＝0的解．

（3）p：四边形两组对边分别平行；q：四边形两组对边分别相等．

（4）p：x2＋x＋1≥0；q：四边形两组对边分别相等．

解（1）因为p真q假，所以，“p或q”为真，“p且q”为假，“非p”为假．

（2）因p假q真，所以，“p或q”为真，“p且q”为假，“非p”为真．

（3）因为p假q假，所以，“p或q”为假，“p且q”为假，“非p”为真．

（4）因为p真q真，所以，“p或q”为真，“p且q”为真，“非p”为假．

例3　填空题：分别用“p或q”“p且q”“非p”填空，并指出命题的真假．

（1）命题“1997年7月1日是中国共产党的生日，又是香港回归祖国的日子”为__________形式，此命题为__________．

（2）命题“方程没有实数根”为___________形式，此命题为___________．

（3）命题“矩形有外接圆或有内切圆”为___________形式，此命题为__________．

（4）命题“A（A∪B）”为__________形式，此命题为___________．

解：（1）“p或q”的形式，其中p：1997年7月1日是中国共产党的生日；q：1997年7月1日是香港回归祖国的日子．因为p真q真，所以“p或q”是真命题．

（2）“非p”的形式，其中p：有实数根．因为p真，所以“非p”是假命题．

（3）“p或q”的形式，其中p：矩形有外接圆；q：矩形有内切圆．因为p真q假（为什么），所以“p或q”是真命题．

（4）“非p”的形式，其中p：A（A∪B）．因为p真，所以“非p”是假命题．

例4　分别指出下列复合命题的形式及构成它的简单命题，并判断它们的真假．

（1）三个角相等的三角形不是直角三角形；

（2）A∩B的元素既是A的元素又是B的元素；

（3）若x是A的元素或x是B的元素，则x是A∪B的元素；

（4）两条对角线垂直的平行四边形是菱形或正方形；

（5）x＝3不是方程｜x－4｜＝1的解．

解：（1）这个命题是“非p”的形式，其中p：三个角相等的三角形是直角三角形．

因为p是假命题，所以这个命题是真命题．

（2）这个命题是“p且q”的形式，其中p：A∩B的元素是A的元素，q：A∩B的元素是B的元素．

因为p、q都是真命题，所以这个命题是真命题．

（3）这个命题是“p或q”的形式，其中p：若x是A的元素，则x是A∪B的元素，q：若x是B的元素，则x是A∪B的元素．

因为p、q都是真命题，所以这个命题是真命题．

（4）这个命题是“p或q”的形式，其中

p：两条对角线垂直的平行四边形是菱形，

q：两条对角线垂直的平行四边形是正方形．

因为p是真命题，q是假命题，所以这个命题是真命题．

（5）这个命题是“非p”的形式，其中

p：x＝3是方程｜x－4｜＝1的解．

因为p是真命题，所以这个命题是假命题．

例5　分别指出由下列各组命题构成的“p或q”、“p且q”、“非p”形式的复合命题的真假．

（1）p：在集合｛x｜0＜x＜2｝中，q：在集合｛x｜x＞1．5｝中．

（2）p：方程x2－3x－1＝0有两正根，q：方程x2－3＝0有两实数根．

（3）p：集合｛x｜1＜x＜2｝是集合｛x｜x＞0｝的子集，q：集合｛x｜1≤x＜2｝是集合｛x｜1＜x＜4｝的子集．

解：（1）因为p为真，而＜1．5，q为假，所以“p或q”为真，“p且q”为假，非p为假．

（2）因为方程x2－3x－1＝0中两根之积为负，所以p为假，q为真，

所以“p或q”为真，“p且q”为假，“非p”为真．

（3）因为p为真，而1｛x｜1＜x＜4｝，所以，｛x｜1≤x＜2｝｛x｜1＜x＜4｝，即q为假．

注：（1）当p、q均为真命题时，“p且q”才为真命题．（2）只要p或q中有一个为真命题，“p或q”必为真命题．即“p或q”为真命题的要求“不高”．

例6　选择题

1．p和q都是简单命题，那么下列结论正确的是（　）．

A．p真，则“p且q”一定真

B．p假，则“p且q”不一定假

C．“p且q”真p一定真

D．“p且q”假，一定假

2．命题“且”与命题“或”都是假命题，那么下列结论正确的是（　）．

A．命题“非p”与命题“非q”其值不同；

B．命题“非p”与命题“非q”至少有一个为假命题；

C．命题“非p且非q”是真命题；

D．命题q与命题“非p”真值相同．

3．若命题“p或q”与命题“p且q”都是真命题，那么下列四个结论中正确的个数是（　）．

①命题q一定是真命题；

②命题q不一定是真命题；

③命题p不一定是真命题；

④命题p与q的真值相同．

A．1　B．2　C．3　D．4

分析：由真值表知：

（1）“非p”形式复合命题的真假与p的真假相反；

（2）“p或q”形式复合命题当p与q同为假时为假，其他情况均为真；

（3）“p且q”形式复合命题当p与q同为真时为真，其他情况均为假．

解：（1）选（C）；（2）选（C）；（3）只有①、④正确．选（B）．