高一数学设计与课例：集合中的元素特性分析

【教学目标】

（1）初步理解集合的概念，掌握其记法及表示方法，掌握常用数集的符号，了解空集概念并掌握其符号；

（2）了解集合中元素的概念，初步了解“属于”关系的意义；

（3）理解集合中元素的确定性、互异性，了解集合中元素的无序性；

（4）初步了解有限集、无限集、空集的意义；

（5）会用集合、元素等知识表示简单集合的有关问题；

（6）渗透数学是来源实践反过来又指导实践的辨证唯物主义观点．

【教学建议】

知识结构

本小节首先从初中代数与几何涉及的集合实例人手，引出集合与集合的元素的概念，并且结合实例对集合的概念作了说明．然后，介绍了集合的常用表示方法，包括列举法、描述法，还给出了画图表示集合的例子．

重点难点分析

这一节的重点是集合的基本概念和表示方法，难点是运用集合的三种常用表示方法正确表示一些简单的集合．这一节的特点是概念多、符号多，正确理解概念和准确使用符号是学好本节的关键．为此，在教学时可以配备一些需要辨析概念、判断符号表示正误的题目，以帮助学生提高判断能力，加深理解集合的概念和表示方法．

1．关于牵头图和引言分析

章头图是一组跳伞队员编成的图案，引言给出了一个实际问题，其目的都是为了引出本章的内容无论是分析还是解决这个实际间题，必须用到集合和逻辑的知识，也就是把它数学化．一方面提高用数学的意识，一方面说明集合和简易逻辑知识是高中数学重要的基础．

2．关于集合的概念分析

点、线、面等概念都是几何中原始的、不加定义的概念，集合则是集合论中原始的、不加定义的概念．

初中代数中曾经了解“正数的集合”、“不等式解的集合”；初中几何中也知道中垂线是“到两定点距离相等的点的集合”等等．在开始接触集合的概念时，主要还是通过实例，对概念有一个初步认识．教科书给出的“一般地，某些指定的对象集在一起就成为一个集合，也简称集．”这句话，只是对集合概念的描述性说明．

我们可以举出很多生活中的实际例子来进一步说明这个概念，从而阐明集合概念如同其他数学概念一样，不是人们凭空想象出来的，而是来自现实世界．

3．关于自然数集的分析

教科书中给出的常用数集的记法，是新的国家标准，与原教科书不尽相同，应该注意．

新的国家标准定义自然数集N含元素0，这样做一方面是为了推行国际标准化组织（ISO）制定的国际标准，以便早日与之接轨，另一方面，0还是十进位数｛0，1，2，…，9｝中最小的数，有了0，减法运算a－a仍属于自然数，其中a∈N．因此要注意几下几点：

（1）自然数集合与非负整数集合是相同的集合，也就是说自然数集包含0；

（2）自然数集内排除0的集，表示成N*或N＋，其他数集｛如整数集Z、有理数集Q、实数集R｝内排除0的集，也可类似表示Z*，Q*，R＋；

（3）原教科书或根据原教科书编写的教辅用书中出现的符号如R＋，Q－，Z＋…不再适用．

4．关于集合中的元素的三个特性分析

集合中的每个对象叫做这个集合的元素．例如“中国的直辖市”这一集合的元素是：北京、上海、天津、重庆．

集合中的元素常用小写的拉丁字母，a，b，c…表示．如果a是集合A的元素，就说a属于集合A，记作；否则，就说a不属于A，记作a∈A；否则，就说a不属于A，记作a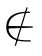A要正确认识集合中元素的特性：

（l）确定性：a∈A和a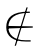A，二者必居其一．

集合中的元素必须是确定的．这就是说，给定一个集合，任何一个对象是不是这个集合的元素也就确定了．例如，给出集合｛地球上的四大洋｝，它的元素是：太平洋、大西洋、印度洋、北冰洋．其他对象都不用于这个集合．如果说“由接近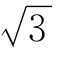的数组成的集合”，这里“接近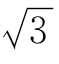的数”是没有严格标准、比较模糊的概念，它不能构成集合．

（2）互异性：若a∈A，b∈A，则a≠b．

集合中的元素是互异的．这就是说，集合中的元素是不能重复的，集合中相同的元素只能算是一个．例如方程x2－2x＋1＝0有两个重根x1＝x2＝1，其解集只能记为｛1｝，而不能记为｛1，1｝．

（3）无序性：｛a，b｝和｛b，a｝表示同一个集合．

集合中的元素是不分顺序的．集合和点的坐标是不同的概念，在平面直角坐标系中，点（l，0）和点（0，l）表示不同的两个点，而集合｛1，0｝和｛0，1｝表示同一个集合．

5．要辩证理解集合和元素这两个概念

（1）集合和元素是两个不同的概念，符号和是表示元素和集合之间关系的，不能用来表示集合之间的关系．例如｛1｝∈｛1，2，3｝的写法就是错误的，而｛1｝∈｛｛1｝，｛2｝，｛3｝｝的写法就是正确的．

（2）一些对象一旦组成了集合，那么这个集合的元素就是这些对象的全体，而非个别现象．例如对于集合｛x∈R｜x≥0｝，就是指所有不小于0的实数，而不是指“x可以在不小于0的实数范围内取值”，不是指“x是不小于0的一个实数或某些实数，”也不是指“x是不小于0的任一实数值”……

（3）集合具有两方面的意义，即：凡是符合条件的对象都是它的元素；只要是它的元素就必须符合条件．

6．表示集合的方法所依据的国家标准

本小节列举法与描述法所使用的集合的记法，依据的是新国家标准如下的规定．

此外，｛x∈A｜p（x）｝有时也可写成｛x∈A∶p（x）｝或｛x∈A；p（x）｝

7．集合的表示方法分析

集合有三种表示方法：列举法、描述法、图示法．它们各有优点．用什么方法来表示集合，要具体问题具体分析．

（l）有的集合可以分别用三种方法表示．例如“小于π的自然数组成的集合”就可以表为：

①列举法：｛0，1，2，3｝；

②描述法：｛0，1，2，3｝；

③图示法：如图1．

（2）有的集合不宜用列举法表示．例如“由小于π的正实数组成的集合”就不宜用列举法表示，因为不能将这个集合中的元素一一列举出来，但这个集合可以这样表示：

①描述法：｛x∈R｜0＜x＜π｝

②图示法：如图2．

（3）用描述法表示集合，要特别注意这个集合中的元素是什么，它应该符合什么条件，从而准确理解集合的意义．例如：

①集合｛x∈R｜y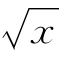＝｝中的元素是x，它表示函数y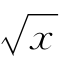＝中自变量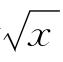的取值范围，即｛x∈R｜x≥0｝；

②集合｛y∈R｜y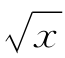＝｝中的元素是y，它表示函数值．的取值范围，即｛y∈R｜y≥0｝；

③集合｛（x，y）｜y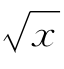＝｝中的元素是点（x，y），它表示方程y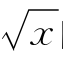＝的解组成的集合，或者理解为表示曲线y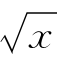＝上的点组成的集合；

④集合｛y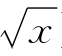＝｝中的元素只有一个，就是方程y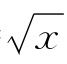＝，它是用列举法表示的单元素集合．

实际上，这是四个完全不同的集合．

列举法与描述法各有优点，应该根据具体问题确定采用哪种表示法．要注意，一般无限集，不宜采用列举法，因为不能将无限集中的元素—一列举出来，而没有列举出来的元素往往难以确定．

8．集合的分类

含有有限个元素的集合叫做有限集，如图1所示．

图　1

含有无限个元素的集合叫做无限集，如图2所示．

图　2

9．关于空集分析

不含任何元素的集合叫做空集，记作Ø．空集是个特殊的集合，除了它本身的实际意义外，在研究集合、集合的运算时，必须予以单独考虑．

【习题精选】

一、选择题

1．下面四个命题正确的是（　）

A．10以内的质数集合是｛0，3，5，7｝

B．“个子较高的人”不能构成集合

C．方程x2－2x＋1＝0的解集是｛1，1｝

D．偶数集为｛x｜x＝2k，x∈N｝

2．下面的结论正确的是（　）

A．ax∈Q，则a∈N

B．a∈N，则a∈｛自然数｝(www.xing528.com)

C．x1－1＝0的解集是｛－1，1｝

D．正偶数集是有限集

【参考答案】

1．B　2．C

二、填空题

1．设P＝｛x｜x≤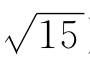｝，m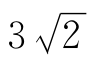＝　则__________P．

2．0___________Ø

3．1___________｛x｜x＝－a2＋1，a∈N＋｝

4．设直线y＝2x＋3上的点集为P，则P___________．点（2，7）与P的关系为（2，7）__________P．

5．集合｛x｜8＜x＜12，x∈N｝，用列举法可表示为___________．

【参考答案】

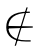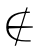1．　2．　3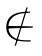．　4．P＝｛（x，y）｜y＝2x＋3｝，（2，7）∈P　5．｛9，10，11｝

三、解答题

1．已知A＝｛（x，y）｜y＝2x－1｝，B＝｛（x，y）｜y＝x＋3｝，a∈A，a∈B，求a

2．已知P＝｛x｜2＜x＜k，x∈N｝，若集合P中恰有3个元素，求k

3．已知集合M＝｛－2，3x2＋3x－4，x2＋x－4｝若2∈M，求满足条件的实数x组成的集合．

4．用适当的方法表示右图中阴影部分的点（含边界上的点）组成的集合M．

【参考答案】

1．a为点（4，7）

2．5＜k≤6

3．｛－3，2｝提示：依题意求出的x要进行检验，不符合集合中元素的特性的应舍去．

【典型例题】

与集合的确定性有关的例题

例1　下列备选项中可以组成集合的是（　）

A．与2非常接近的全体实数

B．很著名的科学家的全体5

C．某教室内的全体桌子

D．与无理数相差很小的数

解：由集合的确定性可知答案为C

与集合相等和空集概念有关的例题

例2　以下说法中正确的个数有（　）

①M＝｛（1，2）｝与N＝｛（2，1）｝表示同一个集合

②M＝｛1，2｝与N＝｛2，1｝表示同一个集合；

③空集是唯一的；

④M＝｛y｜y＝x2＋1，x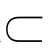R｝与N＝｛x｜x＝t2＋1，t∈R｝，则集合M＝N．

A．3个　B．2个　C．1个　D．0个

解：①集合M表示由点（1，2）组成的单点集，集合N表示点（2，1）组成的单点集．

②由集合元素无序性可知M，N表示同一个集合．

③由Ø1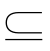Ø2且Ø2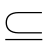Ø1（其中Ø1、Ø2均为空集）由集合相等定义可知Ø1＝Ø2即证明空集唯一性．

④对于要认识一个集合，应从以下方面入手①判断集合元素是什么；②元素有何属性（如表示数集，点集等），表示集合时与代表元素采用的字母无关．而④中的集合都表示大于等于1的实数组成的集合，故相等，选A．

用列举法表示集合

例3　用列举法表示下列集合．

（1）不大于10的质数集合；

（2）｛x｜2≤x≤9，x为偶数｝．

解：（1）不大于10的质数集合是｛2，3，5，7｝．

（2）2≤x≤9，又∵x为偶数，

∴x为2、4、6、8．答案为｛2，4，6，8｝．

用描述法表示集合

例4　用描述法表示下列集合．

（1）正偶数集合；

（2）被3除余1的整数集合；

（3）坐标平面内不在第一、三象限的点集．

解：（1）｛x｜x＝2n，n∈N＋｝；

（2）｛x｜x＝3n＋1，n∈Z｝；

（3）｛（x，y）｜xy≤0｝．

与“属于”符号有关的填空题

例5　用符号“∈”或“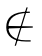”填空．

（1）0____N，－1____N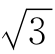____N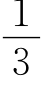，____N；

（2）0____Ø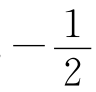____Q，π____Q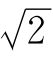____R；

（3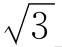____｛x｜x≤2｝；

（4）（1，2）____｛（x，y）｜y＝x＋1｝．

解：（1）∈，，，．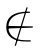

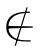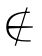（2），，，∈．

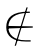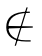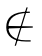（3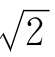）∵＜2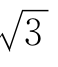，∴∈｛x｜x≤2｝．

（4）点（1，2）在直线y＝x＋1上，而｛（x，y）｜y＝x＋1｝表示直线y＝x＋1上的点集，故（1，2）∈｛（x＋y）｜y＝x＋1｝．

注意：｛x｜x≤2｝表示小于或等于2的实数集，大括号内x∈R一般可以省略，即｛x｜x≤2｝．

集合是一种数学语言，因此，学习集合时，要先理解集合表示的内容及意义，要从语言的角度来学习集合．

集合中元素个数的例题

例6　在实数x，－x，｜x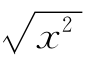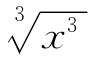｜，，－中选若干数组成集合P，P中元素的个数最多有几个？

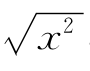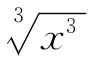解：∵｜x｜＝，－＝－x．

∴x＞0时（x＜0）这列数仅表示两个不同的数，故P中元素的个数最多有2个．