阅读材料题是数学问题里一类拓展性很强的题目，这类题目不止考验学生的数学能力，还要求学生具有很强的阅读理解能力。
进位制是一种计数方式，可以用有限的数字符号代表所有的数值，使用数字符号的数目称为基数，基数为n，即可称n 进制。现在最常用的是十进制，即使用10个阿拉伯数字0～9 进行记数，特点是逢十进一。对于任意一个用n（n ≤10）进制表示的数，通常使用n 个阿拉伯数字0 ～（n-1）进行记数，特点是逢n 进一。例如：五进制数234=2×25+3×5+4=69。
请将五进制数331 和七进制数46 转化为十进制数。
方法点拨
五进制331=3×25+3×5+1=91；
七进制46=4×7+6=34。
❶ 把二进制数100101 转化为十进制数。
❷ 把十进制数20 转化为三进制数。
定义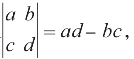
例如
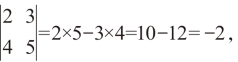若x，y 均为正整数，且满足
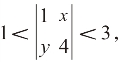则x+y 的值是________。
方法点拨
先根据题意列出不等式，根据x 的取值范围及x 为正整数求出x 的值，再把x 的值代入求出y 的值即可。根据题意得1＜4-xy＜3，得1＜xy＜3，当x=1 时，y=2；当x=2 时，y=1，所以x+y=3。
❶ 对于非零的两个实数a，b，规定a～b 等价于b 的倒数减a 的倒数，若2～（2x-1）=1，求x 的值。
❷ 为确保信息安全，信息需要加密，发送方由明文到密文加密，接收方由密文到明文解密，加密规则：明文a、b、c、d 对应密文a+2b、2b+c、2c+3d、4d，当接收方收到的密文为14、9、23、28 时，明文是什么？
定义一种新法则如下：a……b 等同于a，b 中最大的一个。若（-2m-5）……3=3，求m 的取值范围。
方法点拨
由题意得-2m-5≤3，解得m ≥-4。(www.xing528.com)
❶ 对于不小于3 的自然数n，规定如下一种操作：表示不是n 的约数的最小自然数，如＜7＞=2，＜12＞=5，则＜19＞×＜98＞的值是多少？
❷ 对于任何实数，有a？b=b×b+1，则5？3 的值是多少？
在有理数的范围之内规定一种新运算：a*b=a×a-b×b。求2*5。
方法点拨
2*5=2×2-5×5=-21。
❶ 有一种新定义：对于任何实数a，b，都有a←b=a，a→b=b，则（2006→2005）←（2004→2003）的值是什么？
❷ 在有理数的范围之内规定一种新运算：a＆b@c=（a+b）c。求：5＆2@3。
我国古代数学名著《九章算术》中有这样一道题：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百，善行者追之，几何步及之？”请你用方程组解答这道题。
方法点拨
解：设x 时长能追上，则有（100-60）x=100，
解得：x=2.5，
100×2.5=250，
即250 步能追上。
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》，书中是这样叙述的：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头，从下面数，有94 只脚。问：笼中各有多少只鸡和兔？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
