几何图形是数学中极为重要的一部分。本章将举出一些几何问题的例子，帮助同学们更好地学习这一部分的知识，提高图形理解能力。
如图所示，梯形ABCD 中，AB 平行于CD，又BD=4，AC=3，AB+CD=5。试求梯形ABCD 的面积。
方法点拨
将AB 沿AC 平移至CE，连接BE，在三角形BDE中，有BD=4，BE=AC=3，DE=AB+CD=5，有BD2 +BE2=DE2，所以三角形BDE 为直角三角形。
由于S△ABD=S△ABC=S△BCE，所以梯形ABCD 的面积与三角形BDE 的面积相等，为
❶ 右图是一块长方形草地，长方形的长是16，宽是10。中间有两条道路，一条是长方形，一条是平行四边形，它们的宽都是2，求草地部分的面积（阴影部分）有多大？
❷ 如图所示，一个正十二边形的边长是1 厘米，空白部分是等边三角形，一共有12 个。请算出阴影部分的面积。
下图中每一个小正方形的面积是1 平方厘米，那么格线部分的面积是多少平方厘米？
方法点拨
如图所示，用割补法。格线部分的面积是36 平方厘米。
❶ 图中每一个小正方形的面积是1 平方厘米，那么格线部分的面积是多少平方厘米？
❷ 在一个边长为2 厘米的正方形内，分别以它的三条边为直径向内作三个半圆，则图中阴影部分的面积为________平方厘米。
右图中共有多少个面？多少条棱？
方法点拨
注意：看不见的面和棱都要数出来。9 个面，21 条棱。(https://www.xing528.com)
❶ 如右图，在一个棱长为10 的立方体上截取一个长为8，宽为3，高为2 的小长方体，那么新的几何体的表面积是多少？
❷ 有一个棱长为50 厘米的正方体木块，在它的八个角上各挖去一个棱长为5 厘米的小正方体，那么剩下的立体图形的表面积是多少？
圆柱体的侧面展开，放平，是边长分别为10 厘米和12 厘米的长方形，那么这个圆柱体的体积是________立方厘米。（结果用π 表示）
方法点拨
当圆柱的高是12 厘米时，体积为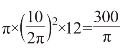
（立方厘米）；
当圆柱的高是10 厘米时，体积为
（立方厘米），所以圆柱体的体积为
立方厘米或
立方厘米。
❶ 如图，有一张长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶（接头处忽略不计），求这个油桶的容积。（π=3.14）
❷ 如图，有一张长方形铁皮，剪下图中两个圆及一块长方形，正好可以做成1 个圆柱体，这个圆柱体的底面半径为10 厘米，那么原来长方形铁皮的面积是多少平方厘米？（π=3.14）
一个酒瓶里面深30cm，底面内直径是10cm，瓶里酒深15cm，把酒瓶塞紧后使其瓶口向下倒立，这时酒深25cm。酒瓶的容积是多少？（π 取3）
方法点拨
观察前后，酒瓶中酒的总量没变，即瓶中液体体积不变。
❶ 一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10 平方厘米（如图所示），请你根据图中标明的数据，计算瓶子的容积是________。
❷ 一个透明的封闭盛水容器，由一个圆柱体和一个圆锥体组成，圆柱体的底面直径和高都是12 厘米。其内有一些水，正放时水面离容器顶11 厘米，倒放时水面离顶部5 厘米，那么这个容器的容积是多少立方厘米？（π 取3）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
