本章主要介绍数论中的基石——数的整除。整除知识点的特点介于“定性分析与定量计算之间”，是很重要的一讲，也是竞赛常考的知识 板块。
若六位数
是13 的倍数，则空格中的数字是几？
方法点拨
解：由于13|78，因此空格中的数是79-78=1。
说明：7，11，13 整除判定性质：
一个数各个位次的数字之和能被9 整除，这个数就能被9 整除；
如果一个整数的末三位与末三位以前的数字组成的数之差能被7，11 或13 整除，那么这个数能被7，11 或13 整除。
❶ 六位数
能被99 整除，
是多少？
❷ 六位数
能被49 整除，
中的数是多少？
173 □是个四位数字。数学老师说：“我在这个空格中先后填入3 个数字，所得到的3 个四位数，依次可被9，11，6 整除。”问：数学老师先后填入的3 个数字的和是多少？
方法点拨
解：用1730 试除，1730÷9=192……2，1730÷1l=157……3，1730÷6=288……2。所以依次添上（9-2=）7，（11-3=）8，（6-2=）4 后得到的1737，1738，1734 依次能被9，11，6 整除。所以，这三种情况下填入□内的数字的和为7+8+4=19。
说明：先试除找出余数再补齐。
❶ 某个七位数
能够同时被2，3，4，5，6，7，8，9 整除，那么它的最后三位数字依次是多少？
❷ 如果六位数
能被105 整除，那么它的最后两位数是多少？
某班同学在班主任老师带领下去种树，学生恰好平均分成三组，如果老师与学生每人种树一样多，共种了1073 棵，那么平均每人种了多少棵树？
方法点拨
解：因为总棵数是每人种的棵数和人数的乘积，所以首先想到的是把1073 化为两个数相乘，即一个数为人数，另一个数为每人种的棵数。1073=37×29，注意到人数减去1 应该是3 的倍数，所以人数是37，平均每人种了29 棵。(www.xing528.com)
说明：利用整除的性质分解因式。
❶ 张老师带领同学们去种树，学生的人数恰好等分成三组。已知老师和学生共种树312 棵，老师与学生每人种的树一样多，并且不超过10 棵。问：一共有多少学生？每人种了几棵树？
❷ 各位数码是0，1 或2，且能被225 整除的最小自然数是多少？
在523 后面写出三个数字，使所得的六位数能分别被7，8，9 整除。这三个数字的和是多少？
方法点拨
解：7、8、9 的最小公倍数是504，所得六位数应被504 整除，则：
524000÷504=1039……344，所以所得六位数是524000-344=523656，或523656-504=523152。因此三个数字的和是17 或8。
说明：根据条件找出最小公倍数，再试除。
❶ 在865 后面补上三个数字，组成一个六位数，使它能分别被3，4，5 整除，且使这个数值尽可能小。
❷ 要使
能被36 整除，而且所得的商最小，那么a，b，c 分别是多少？
在1～2008 这2008 个自然数中，恰好是3，5，7 中两个数的倍数的数共有多少个？
方法点拨
解：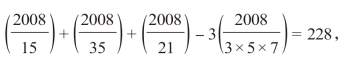
所以共有228 个。
说明：每隔15，35，21 倍数出现一个满足条件的数，还需注意有被重复计算的数（3×5×7），应减去。
❶ 在小于5000 的自然数中，能被11 整除，并且数字之和为13 的数，共有多少个？
❷ 用1，9，8，8 这四个数字能排成几个被11 除余8 的四位数？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
