斐波拉契数列：理解波动规律和市场行为

前面几章对自然法则（波浪理论）的演示有助于我们接下来对后面一些图表的理解。

图68是用半对数刻度画出来的1857年到1932年间的埃克斯—霍顿—伯吉斯指数（Axe-Houghton-Burgess Index）图形。这是目前有记录的最大级数的波浪图形了，从1857年到1928年11月之间，有5个大波浪。这个例子中基准线沿着第2浪和第4浪的底部出现，而平行线则沿着第3浪的顶部出现。第5浪结束时是1928年11月，这时它刚好接触到平行线。

图68

在这整个波浪运动中存在通货膨胀的影响，因此采用对数刻度是非常必要的。但是，如果要单独刻画几轮牛市的图形时，则必须采用算术刻度。

值得注意的是，市场下降到1932年时，指数刚好下降到1896年时的水平，即第5浪的初始点。在这个点位，1929年到1932年间的大崩盘才停止了，也就是说，这是一个正常的调整（a normal correction）。缺乏对过去历史的充分理解导致了人们错误地使用“大萧条（the Great Depression）”这一词汇来形容这段时间的市场情况，所以我特别强调历史在帮助我们理解上面实例以及其他人类活动中的重要性。

图69采用了对数刻度，是图68中对第5浪的分解，刚好也分为5个次级浪。

图69

图70是1921年到1928年间的道琼斯工业指数图，采用的是对数刻度。注意这里沿着第2浪和第4浪画的基准线，以及沿第3浪画的平行线，第5浪的尾部刚好也到达了这根线。(www.xing528.com)

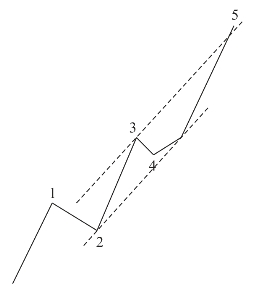
图70

1857年到1928年11月的波浪运动包含了5个波浪，如图68。1896年开始进入第5浪，且这个浪又被细分为5个次级浪，如图69。其中第5个次级浪又可以分解为5个更次级浪，其中的第5浪从1921年开始，如图70。换句话说，从1857年开始的运动可以被分解成三级。

在图71中，道琼斯工业平均指数是按算术刻度绘制的，而波浪1和3的振幅则是波浪5的62%。从1857年到1928年，有7轮牛市和6轮熊市，共计13（又是斐波拉契数列的数字）。所有牛市从1857年到1928年在剧烈程度上是正常的。请记住，从1921年到1928年，有3轮牛市和2轮熊市，而不是1轮牛市。2轮熊市是低于正常水平的。

时间因素是很重要的因素，因为它通常用来确认运动是否符合某种模式。例如，从1928年到1942年共13年（斐波拉契数列的数字），从1937年到1942年是5年（斐波拉契数列的数字）。以上两个期间同时结束。整个运动从1928年到1942年是一个模式，呈三角形。三角形波浪的每一波都是其前一波的62%。所有三个因素——模式、时间和比率都完美地符合斐波拉契求和数列。以上分析见图71。

图71

图72

在前几页中，我们解释了自然法则。总之，斐波拉契数列的数字适用于以下三种方式：波浪的数量、时间（天数、星期数、月份或年份）和比率——62%（斐波拉契数比率）。