计算长方形、正方形面积的方法非常简单:长方形的面积= 长×宽;正方形的面积= 边长×边长。利用它们就可以解决许多有关面积的问题。
当图形比较复杂时,可以通过添加辅助线或运用割补、转化等技巧,化繁为简。因此,敏锐的观察力和灵活的思维在解题过程中十分重要。
把一块长为4 米,宽为3 米的长方形木板,剪成一个面积最大的正方形。这个正方形木板的面积是多少平方米?
要使剪成的正方形面积最大,就要使它的边长最长,那么只能选原来的长方形的宽为边长,即正方形的边长是3 米,如图所示。因此正方形的面积为:3×3=9(平方米)。
❶把一张长为6 厘米,宽为4 厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米?
❷把一块长为2 米,宽为6 厘米的长方形铁板切割成一个面积最大的正方形铁板,这块正方形铁板的面积是多少?
学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20 米。这个花坛的面积是多少平方米?
要求正方形花坛的面积,必须知道花坛的边长是多少。根据绿篱总长是20 米,可求出花坛的边长为:20÷4=5(米),所以花坛的面积是:5×5=25(平方米)。
❶一个正方形的周长为36 厘米,那么这个正方形的面积是多少平方厘米?
❷运动场有一个正方形的游泳池,游泳池的四周贴有瓷砖,瓷砖总长400 米,这个游泳池的面积是多少平方米?
计算下面图形的面积。(单位:厘米)
这个图形无法直接求出它的面积,我们可以画一条辅助线,将这个图形分割成两个长方形,如图所示。从图上可以看出,左边长方形的长为4 厘米,宽为2 厘米,面积为4×2=8(平方厘米);右边长方形的长为3 厘米,宽为1 厘米,面积为3×1=3(平方厘米)。所以,这个图形的面积为:8+3=11(平方厘米)。(https://www.xing528.com)
计算下面图形的面积。(单位:厘米)
❶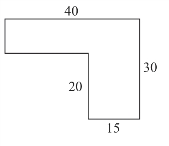 ❷
❷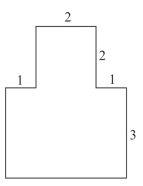
有两个相同的长方形,长是8 厘米,宽是3 厘米。如果把它们按下图叠放,这个图形的面积是多少?
如果两个长方形没有叠放,那么它们的面积就是:8×3×2=48(平方厘米);现在两个长方形重叠了一部分,重叠部分是个边长为3 厘米的正方形,面积是:3×3=9(平方厘米)。所以,这个图形的面积是:48-9=39(平方厘米)。
❶两张边长为8 厘米的正方形纸,一部分叠在一起放在桌上(如下图),桌面被盖住的面积是多少?
❷求下图中阴影部分的面积。(单位:厘米)
一个长方形若长增加2 厘米,则面积就增加10 平方厘米;若宽减少3 厘米,则面积就减少18 平方厘米。求原来长方形的面积。
从右图可以看出,长增加2 厘米,面积就增加10 平方厘米,说明原来长方形的宽是10÷2=5(厘米);宽减少3 厘米,面积就减少18 平方厘米,说明原来长方形的长是18÷3=6(厘米)。所以,原来长方形的面积是:6×5=30(平方厘米)。
❶一个长方形,若宽减少5 厘米,则面积就减少50 平方厘米;若长增加7 厘米,则面积就增加28 平方厘米。原来长方形的面积是多少平方厘米?
❷一个正方形若边长都增加4 厘米,则面积就增加56 平方厘米。原来正方形的面积是多少平方厘米?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




